2011:Query-by-Singing/Humming Results

Introduction

These are the results for the 2008 running of the Query-by-Singing/Humming task. For background information about this task set please refer to the 2011:Query by Singing/Humming page.

Task Descriptions

Task 1 Goto Task 1 Results: The first subtask is the same as last year. In this subtask, submitted systems take a sung query as input and return a list of songs from the test database. Mean reciprocal rank (MRR) of the ground truth, as well as the simple hit(1)/miss(0) counting, is calculated over the top 10 returns. Two data sets are used:

• Jang's Dataset Results Roger Jang's MIR-QBSH corpus with 48 songs as ground truth + 2000 Essen Collection MIDI noise files. See ESAC Data Homepage for more information about the Essen Collection. The queries consists of 4431 humming. All queries are from the beginning of references
• ThinkIT's Dataset Results IOACAS corpus 1 data set with 106 songs as ground truth + 2000 Essen Collection MIDI noise files. See ESAC Data Homepage for more information about the Essen Collection. The queries consists of 355 humming. There are no "singing from beginning" gurantee.
• IOACAS's 2nd Dataset Results IOACAS corpus 2 data set with 192 songs as ground truth + 2000 Essen Collection MIDI noise files. See ESAC Data Homepage for more information about the Essen Collection. The queries consists of 404 humming. There are no "singing from beginning" gurantee.

Task 2 Goto Task 2 Results: The second subtask is the query against other humming. In the second subtask, Roger Jang's MIR-QBSH corpus has been divided into two groups (2040 as queries and 2391 as database). The query is performed against the other humming database and the top 10 closed are returned. The score is simple count of how many returns belong to the same ground truth song.

General Legend

Sub code	Submission name	Abstract	Contributors
HAFR1	QBH Simbals	PDF	Pierre Hanna, Julien Allali, Pascal Ferraro, Matthias Robine
JY1	The programs of QBSH -beginning	PDF	Jingzhou Yang
JY2	The programs of QBSH -anywhere	PDF	Jingzhou Yang
YF1	Yeh, Fang -beginning	PDF	Tzu-chun Yeh, Yi-fan Fang
YF2	Yeh, Fang -anywhere	PDF	Tzu-chun Yeh, Yi-fan Fang

Task 1 Results

Task 1a, Jang's dataset Results

Task 1a Overall Results

	JSSLP1	TY1	TY2
Simple Count	0.939	0.956	0.919
MRR	0.897	0.93	0.881
Total Count	4431	4431	4431

download these results as csv

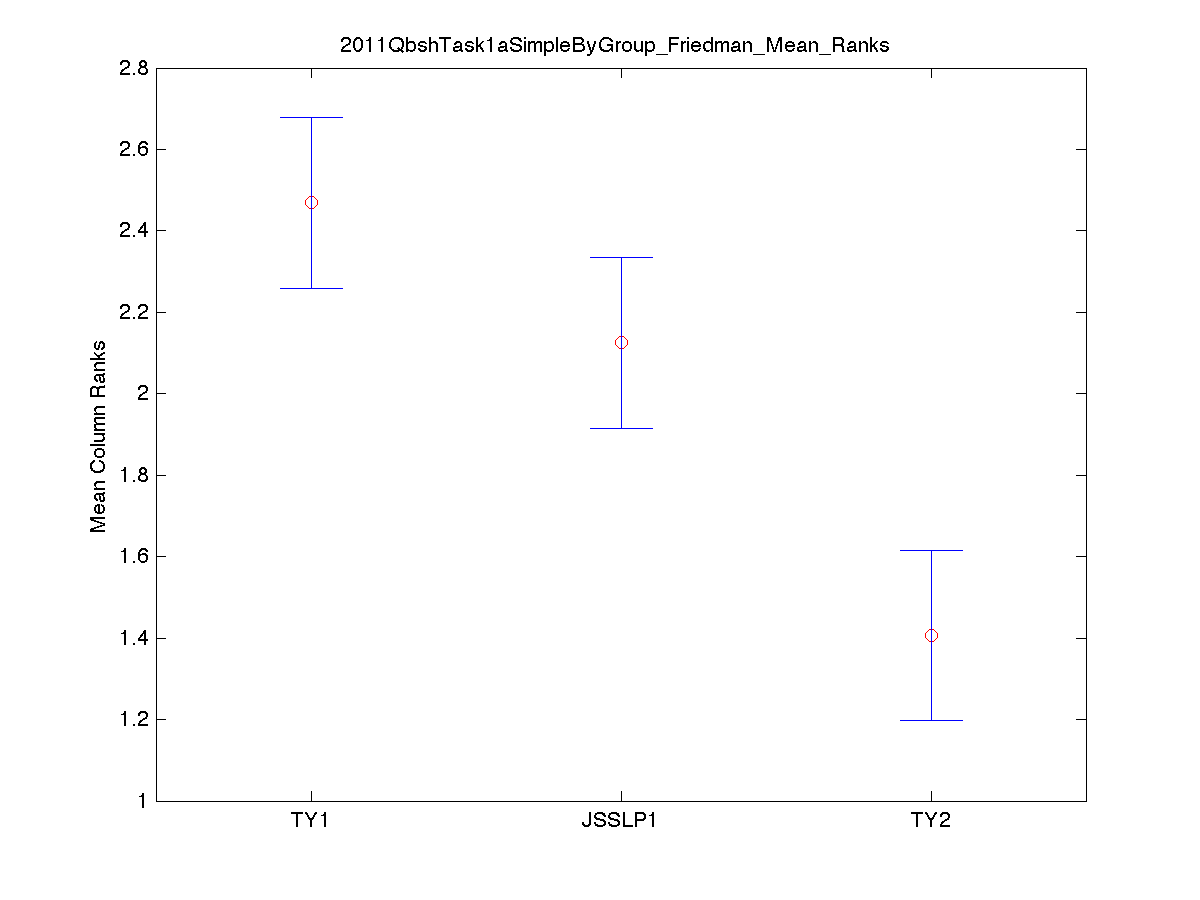
Task 1a Friedman's Test for Significant Differences

The Friedman test was run in MATLAB against the QBSH Task 1a Simple/MRR data over the 48 ground truth song groups. Command: [c,m,h,gnames] = multcompare(stats, 'ctype', 'tukey-kramer','estimate', 'friedman', 'alpha', 0.05);

Simple Hit/Miss Count:

TeamID	TeamID	Lowerbound	Mean	Upperbound	Significance
TY1	JSSLP1	-0.0749	0.3438	0.7624	FALSE
TY1	TY2	0.6439	1.0625	1.4811	TRUE
JSSLP1	TY2	0.3001	0.7188	1.1374	TRUE

download these results as csv

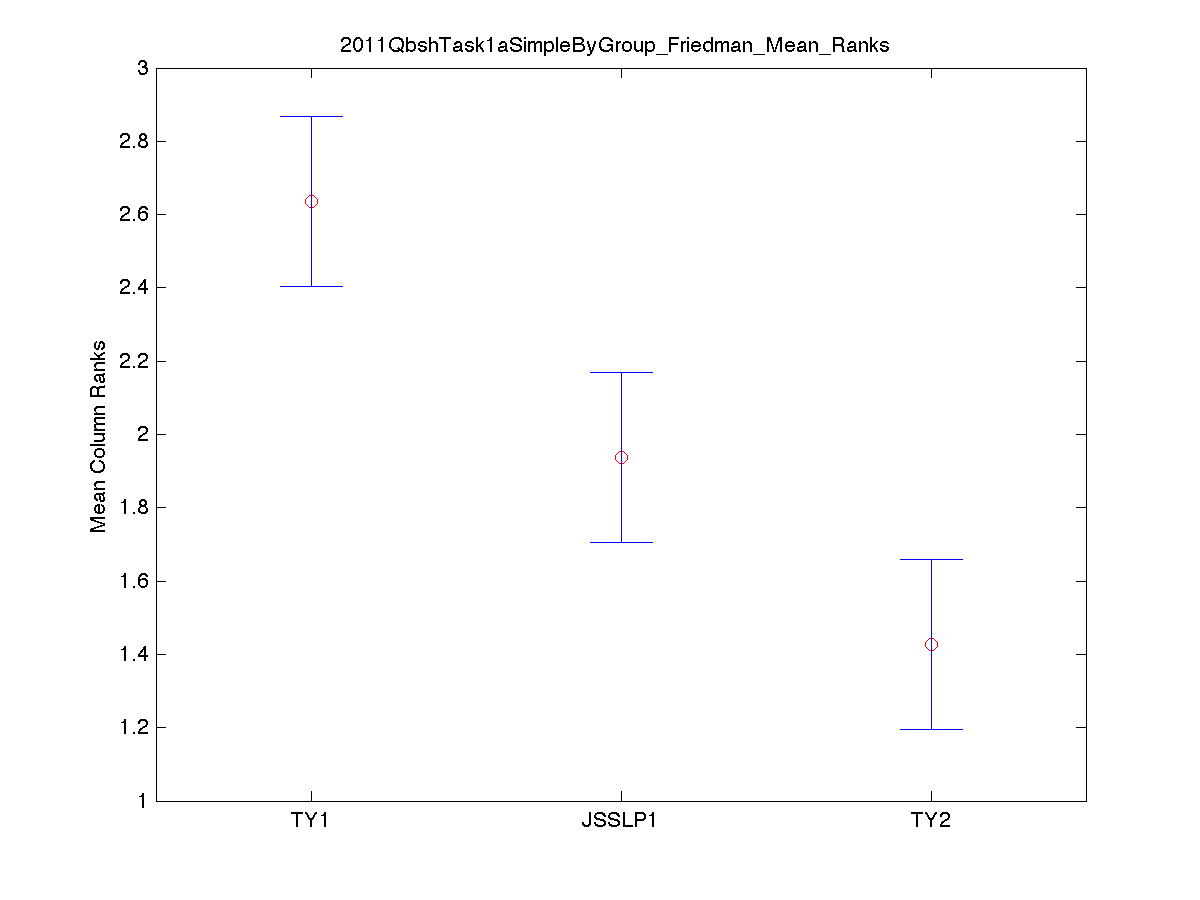
MRR Method:

TeamID	TeamID	Lowerbound	Mean	Upperbound	Significance
TY1	JSSLP1	0.2321	0.6979	1.1637	TRUE
TY1	TY2	0.7426	1.2083	1.6741	TRUE
JSSLP1	TY2	0.0446	0.5104	0.9762	TRUE

download these results as csv

Task 1a Summary Results by Query Group

Simple Hit/Miss Count

	JSSLP1	TY1	TY2
1	0.947	0.947	0.895
2	0.714	0.786	0.643
3	0.727	0.727	0.727
4	0.8	0.8	0.8
5	0.933	0.933	0.8
6	0.833	0.833	0.917
7	0.867	0.933	0.867
8	0.933	0.933	0.933
9	0.917	0.917	0.917
10	0.947	0.684	0.842
11	0.927	0.948	0.896
12	0.968	0.968	0.961
13	0.95	0.981	0.963
14	0.975	0.994	0.956
15	0.963	0.963	0.963
16	0.931	0.969	0.925
17	0.941	0.98	0.928
18	0.97	0.976	0.957
19	0.949	0.968	0.943
20	0.971	1	0.982
21	0.742	0.818	0.758
22	0.977	0.988	0.977
23	1	0.984	0.952
24	0.752	0.843	0.785
25	0.756	0.862	0.715
26	0.962	0.962	0.962
27	0.965	0.965	0.965
28	0.879	0.879	0.725
29	0.993	0.987	0.973
30	0.959	0.986	0.938
31	0.979	0.993	0.972
32	0.964	0.956	0.934
33	0.94	0.94	0.862
34	0.949	0.927	0.891
35	0.926	0.966	0.886
36	0.953	0.93	0.953
37	0.939	0.939	0.848
38	0.965	0.93	0.956
39	0.952	0.98	0.939
40	0.93	0.972	0.915
41	0.944	0.984	0.913
42	0.957	0.946	0.946
43	0.951	0.976	0.943
44	0.95	0.95	0.95
45	0.97	0.97	0.939
46	0.989	0.978	0.935
47	0.931	1	0.931
48	0.962	1	0.925

download these results as csv

MRR Method

	JSSLP1	TY1	TY2
1	0.947	0.901	0.847
2	0.714	0.732	0.595
3	0.682	0.682	0.645
4	0.8	0.8	0.8
5	0.933	0.85	0.767
6	0.833	0.833	0.808
7	0.867	0.889	0.867
8	0.933	0.88	0.933
9	0.917	0.917	0.844
10	0.947	0.61	0.842
11	0.876	0.932	0.868
12	0.945	0.958	0.937
13	0.917	0.94	0.938
14	0.865	0.969	0.879
15	0.944	0.907	0.93
16	0.889	0.922	0.891
17	0.905	0.95	0.857
18	0.959	0.965	0.947
19	0.931	0.968	0.925
20	0.929	0.977	0.944
21	0.632	0.722	0.678
22	0.973	0.984	0.966
23	0.965	0.962	0.939
24	0.688	0.78	0.694
25	0.541	0.79	0.595
26	0.942	0.946	0.939
27	0.928	0.965	0.951
28	0.776	0.798	0.597
29	0.953	0.968	0.959
30	0.934	0.969	0.91
31	0.965	0.988	0.944
32	0.93	0.956	0.891
33	0.886	0.92	0.802
34	0.882	0.908	0.85
35	0.887	0.948	0.876
36	0.935	0.93	0.953
37	0.908	0.903	0.833
38	0.949	0.906	0.923
39	0.921	0.946	0.882
40	0.878	0.914	0.866
41	0.922	0.948	0.898
42	0.895	0.935	0.91
43	0.925	0.943	0.904
44	0.923	0.944	0.938
45	0.962	0.954	0.916
46	0.913	0.948	0.92
47	0.931	0.955	0.931
48	0.945	0.95	0.915

download these results as csv

Task 1a Summary Results by Query

Simple Hit/Miss Counting [1]

MRR Method [2]

Task 1b, ThinkIT's dataset Results

Task 1b Overall Results

	JSSLP1	TY1	TY2
Simple Count	0.941	0.456	0.899
MRR	0.912	0.437	0.853
Total Count	355	355	355

download these results as csv

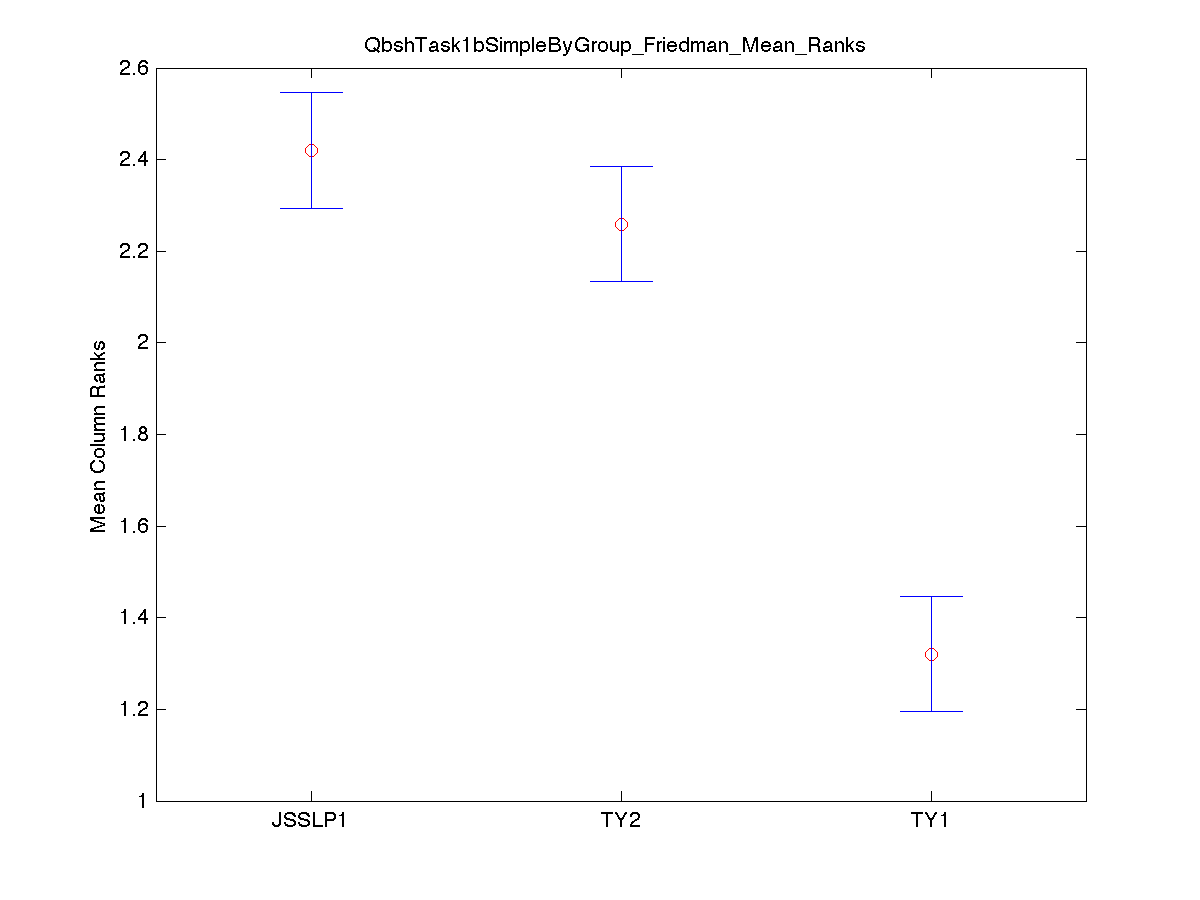
Task 1b Friedman's Test for Significant Differences

The Friedman test was run in MATLAB against the QBSH Task 1b Simple/MRR data over the 106 ground truth song groups. Command: [c,m,h,gnames] = multcompare(stats, 'ctype', 'tukey-kramer','estimate', 'friedman', 'alpha', 0.05);

Simple Hit/Miss Count:

TeamID	TeamID	Lowerbound	Mean	Upperbound	Significance
JSSLP1	TY2	-0.0922	0.1604	0.4130	FALSE
JSSLP1	TY1	0.8465	1.0991	1.3516	TRUE
TY2	TY1	0.6861	0.9387	1.1913	TRUE

download these results as csv

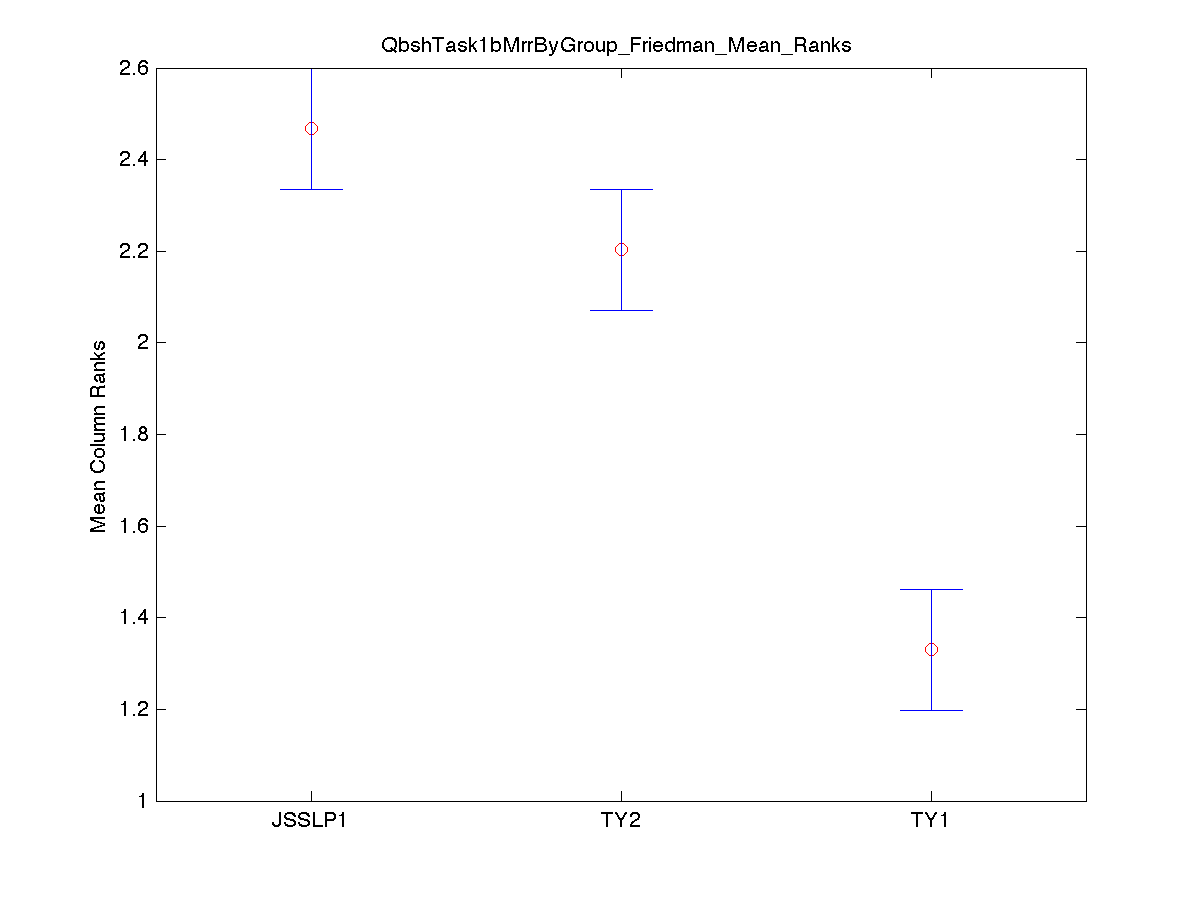
MRR Method:

TeamID	TeamID	Lowerbound	Mean	Upperbound	Significance
JSSLP1	TY2	0.0002	0.2642	0.5281	TRUE
JSSLP1	TY1	0.8729	1.1368	1.4007	TRUE
TY2	TY1	0.6087	0.8726	1.1366	TRUE

download these results as csv

Task 1b Summary Results by Query Group

Simple Hit/Miss Count

	JSSLP1	TY1	TY2
1	1	0.636	1
2	1	0.6	0.8
3	0	0	1
4	1	1	1
5	0	0	1
6	0.833	0	0.667
7	1	1	1
8	1	0.333	0.667
9	1	0	1
10	1	0	1
11	1	0	0.5
12	1	1	1
13	0.8	0.2	0.6
14	1	0	1
15	1	0	0.5
16	1	1	0.75
17	0	0	0
18	1	0.5	1
19	1	0	1
20	1	0	0.5
21	1	0	0.5
22	1	0.444	0.889
23	1	1	1
24	1	0	1
25	1	0.5	1
26	1	0.636	0.909
27	1	0.5	1
28	1	0.5	0.75
29	1	1	1
30	1	1	1
31	1	1	1
32	1	0	1
33	1	0	1
34	0.5	0.5	0.5
35	1	0	1
36	0.8	0	0.8
37	1	0	0
38	1	0.5	1
39	1	0.429	1
40	1	1	1
41	0.875	0.25	0.875
42	1	0.667	0.917
43	0.889	0.667	0.778
44	1	0.556	1
45	1	1	1
46	0.75	0.5	0.75
47	1	0.75	1
48	1	1	1
49	1	1	1
50	1	1	1
51	1	0.5	1
52	1	0.5	0.75
53	1	0.333	1
54	1	0.833	1
55	1	0	1
56	0.5	0.5	0.5
57	1	1	1
58	1	0	1
59	1	0	1
60	0	1	1
61	1	0	1
62	1	0.333	1
63	1	1	1
64	1	0	1
65	1	0	0.667
66	1	0.5	0.75
67	0.333	0	1
68	1	1	1
69	1	0	1
70	1	1	1
71	1	0	1
72	1	1	1
73	1	1	1
74	1	1	1
75	1	0.333	0.667
76	0.5	0	1
77	1	1	1
78	1	1	1
79	1	0.5	1
80	0.333	0.333	1
81	1	0.333	1
82	1	0	1
83	1	0	1
84	0.75	0.25	0.5
85	1	0.5	1
86	1	1	1
87	1	0	1
88	1	0	1
89	1	0.571	0.714
90	1	0	1
91	1	0	1
92	1	0.5	1
93	1	0.5	1
94	1	0	1
95	1	0	1
96	1	1	0
97	1	0	1
98	1	0	1
99	1	0.75	1
100	1	0.333	1
101	0	0	0
102	1	0	1
103	1	0.375	1
104	1	0	1
105	1	1	0
106	0.667	0	0.667

download these results as csv

MRR Method

	JSSLP1	TY1	TY2
1	1	0.5	1
2	1	0.6	0.8
3	0	0	1
4	0.667	0.163	0.563
5	0	0	0.25
6	0.75	0	0.667
7	1	1	0.917
8	1	0.333	0.667
9	1	0	0.9
10	1	0	1
11	1	0	0.5
12	1	1	1
13	0.8	0.2	0.6
14	1	0	0.625
15	0.667	0	0.5
16	1	1	0.542
17	0	0	0
18	1	0.5	1
19	1	0	1
20	0.375	0	0.1
21	1	0	0.083
22	0.926	0.389	0.806
23	1	1	1
24	1	0	1
25	1	0.5	1
26	1	0.636	0.909
27	1	0.5	1
28	1	0.375	0.75
29	1	1	1
30	1	1	1
31	1	1	1
32	1	0	1
33	0.9	0	1
34	0.5	0.5	0.5
35	1	0	1
36	0.8	0	0.8
37	0.333	0	0
38	1	0.5	1
39	1	0.429	1
40	1	1	1
41	0.875	0.167	0.875
42	1	0.667	0.917
43	0.833	0.667	0.722
44	1	0.556	1
45	1	1	1
46	0.625	0.5	0.75
47	1	0.75	1
48	1	1	1
49	1	1	1
50	1	1	1
51	1	0.5	0.75
52	1	0.281	0.75
53	1	0.333	0.861
54	1	0.75	1
55	1	0	1
56	0.5	0.5	0.5
57	1	1	1
58	1	0	1
59	1	0	1
60	0	1	1
61	1	0	0.25
62	1	0.333	1
63	1	1	1
64	1	0	1
65	1	0	0.667
66	1	0.5	0.75
67	0.333	0	1
68	0.625	1	0.556
69	1	0	1
70	1	1	1
71	1	0	0.722
72	1	1	1
73	1	1	1
74	1	1	1
75	1	0.333	0.444
76	0.5	0	1
77	1	1	1
78	1	1	1
79	1	0.5	1
80	0.333	0.333	1
81	1	0.333	0.857
82	1	0	1
83	0.833	0	0.611
84	0.55	0.125	0.5
85	1	0.5	1
86	1	1	1
87	1	0	1
88	1	0	1
89	0.881	0.571	0.643
90	1	0	1
91	1	0	1
92	1	0.5	1
93	1	0.5	1
94	1	0	1
95	1	0	1
96	1	1	0
97	1	0	1
98	1	0	1
99	1	0.75	1
100	1	0.333	1
101	0	0	0
102	1	0	1
103	1	0.375	0.938
104	1	0	1
105	0.25	1	0
106	0.444	0	0.333

download these results as csv

Task 1b Summary Results by Query

Simple Hit/Miss Counting [3]

MRR Method [4]

Task 1c, IOACAS2's dataset Results

As argued by Jang, there are some abnormal in the IOACAS2 data set. Therefore, we just provide the raw result without any further analysis.

Task 1c Summary Results by Query Group

Simple Hit/Miss Count

	JSSLP1	TY1	TY2
1	0	0	1
2	0	0	0
3	1	0	1
4	0	0	0
5	0.182	0.273	0.273
6	0	0	0
7	0	0.5	0.5
8	0	0	0
9	0	1	0
10	1	1	1
11	0	0	0.5
12	1	0	1
13	0	0.143	0.286
14	0.2	0.2	0.4
15	0	0	0
16	0	1	1
17	0	0	0
18	0	0	1
19	0	0	0.5
20	0	0.5	0
21	0	0	0.5
22	0	0	0
23	0	0	0
24	0	0	0
25	0	0	0
26	0	0	0.25
27	0	0	0
28	0	0	0
29	0.125	0.375	0.375
30	1	0	0
31	0	0	0
32	0	0	0
33	0	0.333	0.333
34	0	0	0
35	0	1	1
36	0	0.5	0
37	0.111	0	0.556
38	0	0.5	0.5
39	0	0	1
40	0.5	0.5	0.5
41	1	1	1
42	0	0	0
43	0	0	0
44	0.5	0.5	1
45	0	0	0
46	0	0	0
47	0	0	1
48	0	0	1
49	0	0	0
50	0.375	0.375	0.25
51	0	0.25	0.25
52	0	0.333	0.333
53	0	0	0.5
54	0.5	0	0.25
55	1	0	0
56	1	0.667	0.333
57	0.333	0	0.333
58	0	0	0
59	0	1	1
60	1	0	1
61	0	0	0.5
62	0	0	0
63	1	0	0
64	0.333	0.333	0.333
65	1	1	0
66	1	0	0
67	0.5	0	0
68	1	0.6	0.6
69	1	0	0.333
70	0.6	0	0.7
71	1	0	0
72	0.833	0.667	0.5
73	0	0	0
74	0.333	0	0
75	0.5	0	0
76	0	0	0
77	1	1	0
78	0.667	0.833	0.5
79	0	0	0
80	0.615	0.615	0.692
81	0.2	0	0
82	0	0	0
83	0.571	0.857	0.143
84	0	0	0
85	1	0	0
86	1	0	1
87	1	1	1
88	0.25	0.25	0.75
89	1	0	1
90	0	0	0
91	0.5	0.5	0.5
92	1	0.5	1
93	1	0.4	0.8
94	0	1	0
95	0	0	1
96	0.667	0.667	0.333
97	1	0	1
98	1	1	1
99	0	1	0
100	0	0	0.5
101	0	0	1
102	0.875	0.5	0.375
103	1	0	1
104	1	1	0
105	1	0	1
106	0	0	0
107	0.5	0	1
108	1	0	1
109	1	1	0.5
110	0	0	1
111	0	0	0
112	0	0	0
113	0	0	0
114	1	1	1
115	1	1	0
116	0	0.5	0
117	0	0	0
118	1	1	0
119	0	0.2	0.2
120	0	0	0
121	0	0	0
122	1	1	0
123	1	0	1
124	0	0	0
125	1	0.5	1
126	0	0	0
127	0	0	0
128	0	0	0
129	1	0	1
130	0	0	0
131	0	1	1
132	0	0	0.5
133	1	1	1
134	1	1	1
135	1	0	0
136	1	0	1
137	1	0	1
138	1	0	0.667
139	1	1	1
140	1	1	0
141	1	1	1
142	1	0	0.75
143	1	0	0
144	1	0	0
145	0.333	0.333	0.333
146	0	0	0
147	1	0	1
148	1	0.5	1
149	1	1	1
150	1	0.5	1
151	1	0	1
152	0.667	0.333	0.333
153	1	0	0
154	1	0	1
155	0	0	1
156	1	1	0
157	1	1	1
158	0	0	0
159	0	0	0
160	0	0	0
161	0	1	0
162	0	1	0
163	0	0	0
164	1	0	1
165	1	0	0
166	0	0	0
167	1	1	1
168	1	1	1
169	1	1	1
170	1	1	1
171	0	0	0
172	1	1	1
173	1	1	1
174	1	1	0
175	1	0	1
176	1	0	1
177	0	0	0
178	1	1	0.5
179	1	1	1
180	1	0	0
181	1	1	1
182	1	0	0
183	1	0	1
184	0	0	1
185	0	1	1
186	1	0	0.667
187	1	0	1
188	0	1	0
189	0	0	1
190	1	0.5	1
191	1	1	0
192	0	0	1

download these results as csv

MRR Method

	JSSLP1	TY1	TY2
1	0	0	1
2	0	0	0
3	1	0	1
4	0	0	0
5	0.025	0.132	0.133
6	0	0	0
7	0	0.5	0.083
8	0	0	0
9	0	1	0
10	1	1	1
11	0	0	0.3
12	1	0	1
13	0	0.143	0.163
14	0.04	0.022	0.073
15	0	0	0
16	0	1	0.5
17	0	0	0
18	0	0	0.2
19	0	0	0.071
20	0	0.092	0
21	0	0	0.063
22	0	0	0
23	0	0	0
24	0	0	0
25	0	0	0
26	0	0	0.042
27	0	0	0
28	0	0	0
29	0.042	0.375	0.292
30	0.333	0	0
31	0	0	0
32	0	0	0
33	0	0.167	0.083
34	0	0	0
35	0	0.1	1
36	0	0.5	0
37	0.037	0	0.347
38	0	0.5	0.167
39	0	0	0.5
40	0.5	0.5	0.25
41	1	0.1	0.5
42	0	0	0
43	0	0	0
44	0.5	0.5	0.75
45	0	0	0
46	0	0	0
47	0	0	0.25
48	0	0	0.5
49	0	0	0
50	0.156	0.153	0.104
51	0	0.025	0.25
52	0	0.333	0.111
53	0	0	0.5
54	0.5	0	0.031
55	1	0	0
56	1	0.25	0.167
57	0.333	0	0.042
58	0	0	0
59	0	1	1
60	1	0	1
61	0	0	0.25
62	0	0	0
63	1	0	0
64	0.333	0.333	0.235
65	0.25	0.5	0
66	1	0	0
67	0.167	0	0
68	0.808	0.511	0.448
69	1	0	0.167
70	0.513	0	0.7
71	1	0	0
72	0.833	0.542	0.357
73	0	0	0
74	0.063	0	0
75	0.125	0	0
76	0	0	0
77	1	0.333	0
78	0.431	0.597	0.274
79	0	0	0
80	0.492	0.547	0.564
81	0.1	0	0
82	0	0	0
83	0.214	0.619	0.048
84	0	0	0
85	1	0	0
86	1	0	0.813
87	0.143	1	0.333
88	0.25	0.25	0.625
89	1	0	1
90	0	0	0
91	0.5	0.5	0.5
92	1	0.5	1
93	0.867	0.4	0.65
94	0	0.143	0
95	0	0	0.143
96	0.667	0.667	0.333
97	1	0	0.6
98	1	1	0.583
99	0	1	0
100	0	0	0.167
101	0	0	0.1
102	0.688	0.5	0.375
103	1	0	1
104	0.143	1	0
105	1	0	1
106	0	0	0
107	0.063	0	1
108	1	0	0.333
109	0.75	1	0.5
110	0	0	0.5
111	0	0	0
112	0	0	0
113	0	0	0
114	1	1	1
115	1	0.75	0
116	0	0.5	0
117	0	0	0
118	1	0.333	0
119	0	0.1	0.2
120	0	0	0
121	0	0	0
122	0.143	1	0
123	1	0	0.333
124	0	0	0
125	1	0.063	1
126	0	0	0
127	0	0	0
128	0	0	0
129	0.111	0	1
130	0	0	0
131	0	1	1
132	0	0	0.167
133	0.5	1	1
134	1	1	1
135	0.5	0	0
136	1	0	1
137	0.143	0	0.143
138	0.833	0	0.278
139	1	1	1
140	1	0.5	0
141	1	1	1
142	0.708	0	0.165
143	1	0	0
144	1	0	0
145	0.333	0.333	0.333
146	0	0	0
147	0.25	0	0.5
148	1	0.5	1
149	1	1	1
150	0.571	0.5	0.5
151	1	0	0.5
152	0.444	0.111	0.333
153	1	0	0
154	0.25	0	0.5
155	0	0	0.2
156	0.2	1	0
157	1	1	1
158	0	0	0
159	0	0	0
160	0	0	0
161	0	0.25	0
162	0	0.333	0
163	0	0	0
164	0.333	0	1
165	1	0	0
166	0	0	0
167	0.5	1	1
168	1	1	0.5
169	1	1	1
170	1	1	0.167
171	0	0	0
172	1	1	1
173	1	1	1
174	1	0.111	0
175	1	0	0.5
176	1	0	0.5
177	0	0	0
178	0.625	1	0.063
179	1	1	1
180	0.5	0	0
181	1	1	1
182	1	0	0
183	1	0	1
184	0	0	1
185	0	0.125	0.333
186	1	0	0.5
187	1	0	0.333
188	0	0.125	0
189	0	0	1
190	1	0.5	0.417
191	1	0.5	0
192	0	0	1

download these results as csv

Task 1c Summary Results by Query

Simple Hit/Miss Counting [5]

MRR Method [6]

Task 2 Results

Task 2 Overall Results

	JSSLP1	TY1	TY2
Multi Count	9.275	8.744	8.744
Total Count	2040	2040	2040

download these results as csv

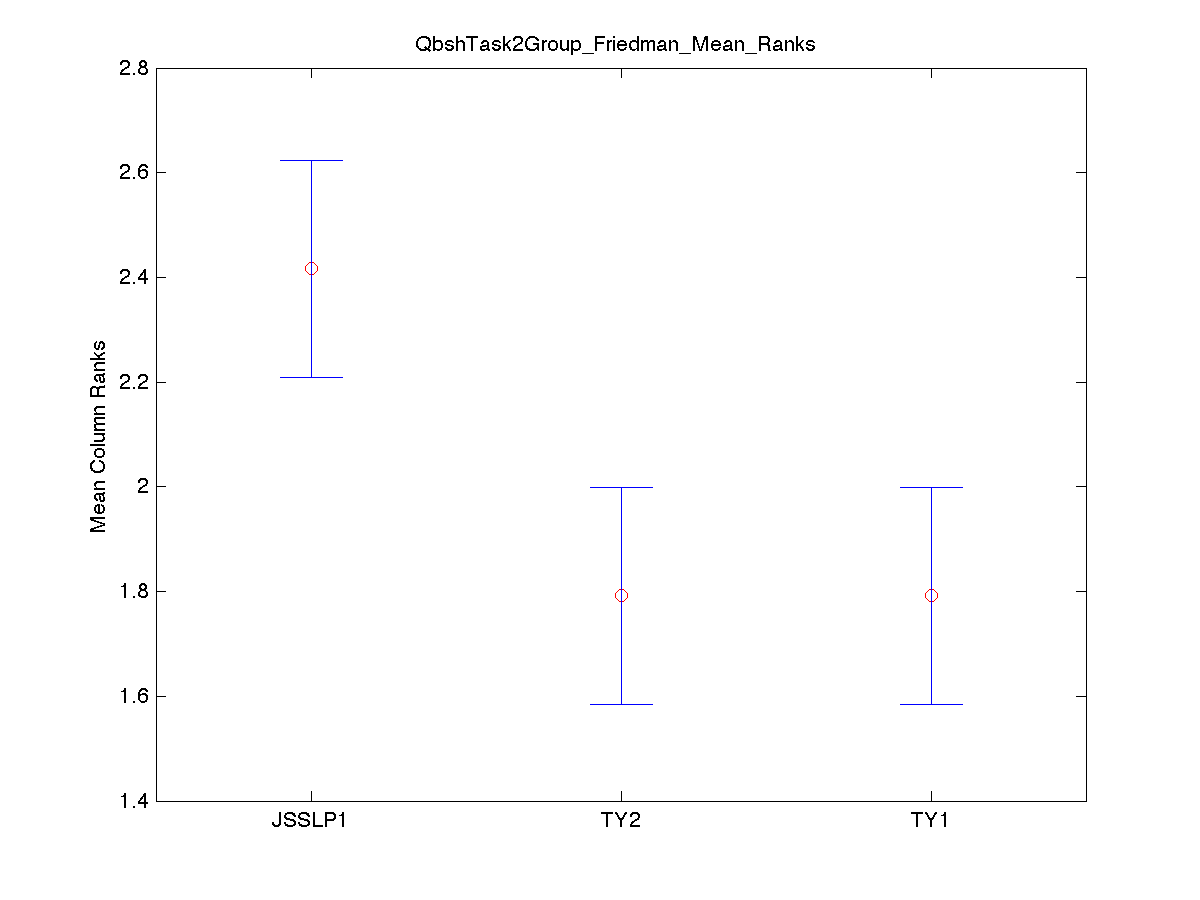
Task 2 Friedman's Test for Significant Differences

The Friedman test was run in MATLAB against the QBSH Task 2 data over the 48 ground truth song groups. Command: [c,m,h,gnames] = multcompare(stats, 'ctype', 'tukey-kramer','estimate', 'friedman', 'alpha', 0.05);

TeamID	TeamID	Lowerbound	Mean	Upperbound	Significance
JSSLP1	TY2	0.2107	0.6250	1.0393	TRUE
JSSLP1	TY1	0.2107	0.6250	1.0393	TRUE
TY2	TY1	-0.4143	0.0000	0.4143	FALSE

download these results as csv

Task 2 Summary Results by Query Group

	JSSLP1	TY1	TY2
1	5.889	5.333	5.333
2	2.000	2.250	2.250
3	4.000	0.000	0.000
4	3.200	4.400	4.400
5	7.000	6.800	6.800
6	3.000	5.000	5.000
7	2.800	6.600	6.600
8	8.600	6.800	6.800
9	3.500	2.000	2.000
10	5.889	4.556	4.556
11	9.349	8.791	8.791
12	9.222	9.542	9.542
13	9.145	9.237	9.237
14	9.625	8.722	8.722
15	8.071	5.214	5.214
16	9.757	8.932	8.932
17	9.167	9.181	9.181
18	9.789	9.026	9.026
19	9.478	9.333	9.333
20	9.659	9.341	9.341
21	8.735	8.971	8.971
22	9.663	9.398	9.398
23	9.581	8.516	8.516
24	8.898	9.136	9.136
25	8.898	8.119	8.119
26	9.095	7.619	7.619
27	9.267	8.156	8.156
28	9.152	9.043	9.043
29	9.956	9.426	9.426
30	9.418	9.687	9.687
31	9.800	9.650	9.650
32	9.484	9.719	9.719
33	8.980	7.824	7.824
34	9.721	9.456	9.456
35	9.710	8.971	8.971
36	7.167	7.833	7.833
37	8.893	7.250	7.250
38	9.741	8.593	8.593
39	9.662	7.574	7.574
40	9.481	8.815	8.815
41	9.136	9.322	9.322
42	9.071	7.119	7.119
43	9.483	8.483	8.483
44	8.778	9.361	9.361
45	9.574	7.298	7.298
46	9.368	8.368	8.368
47	8.769	8.231	8.231
48	8.636	8.364	8.364

download these results as csv

Task 2 Summary Results by Query

[7]

Runtime Results

file /nema-raid/www/mirex/results/2011/qbsh/QbshRunTime.csv not found