Difference between revisions of "2017:Discovery of Repeated Themes & Sections Results"
(→Introduction) |
(→SymMono) |
||
| Line 141: | Line 141: | ||
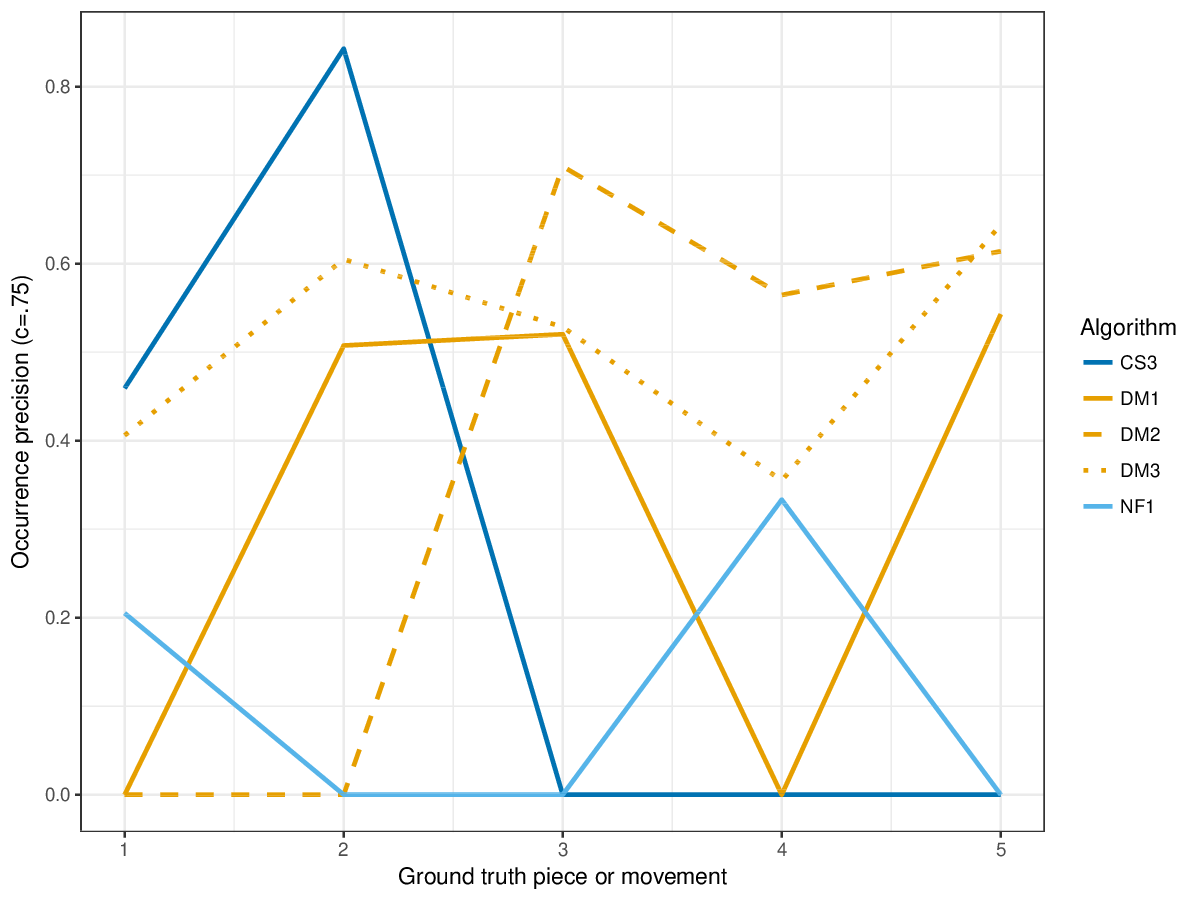
'''Figure 5.''' Occurrence precision (<math>c = .75</math>) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences? | '''Figure 5.''' Occurrence precision (<math>c = .75</math>) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences? | ||
| − | [[File: | + | [[File:Mono_F1_occ_75.png|600px]] |
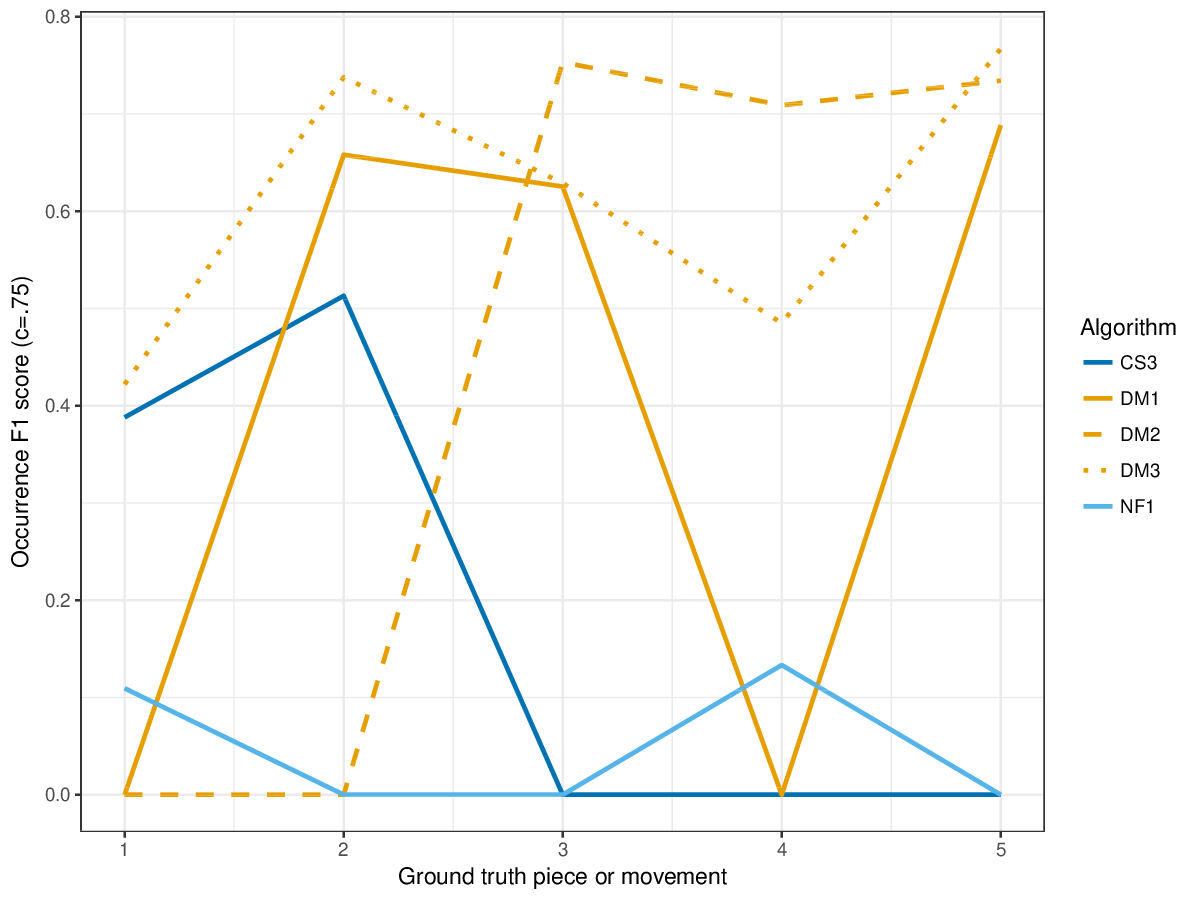
'''Figure 6.''' Occurrence F1 (<math>c = .75</math>) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall. | '''Figure 6.''' Occurrence F1 (<math>c = .75</math>) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall. | ||
Revision as of 04:33, 15 October 2017
THIS PAGE IS UNDER CONSTRUCTION
Contents
Introduction
The task: algorithms take a piece of music as input, and output a list of patterns repeated within that piece. A pattern is defined as a set of ontime-pitch pairs that occurs at least twice (i.e., is repeated at least once) in a piece of music. The second, third, etc. occurrences of the pattern will likely be shifted in time and/or transposed, relative to the first occurrence. Ideally an algorithm will be able to discover all exact and inexact occurrences of a pattern within a piece, so in evaluating this task we are interested in both:
- (1) to what extent an algorithm can discover one occurrence, up to time shift and transposition;
- (2) to what extent it can find all occurrences, and;
- (3) to what extent repeated patterns discovered by an algorithm allow for compression of a melody.
The metrics establishment recall, establishment precision and establishment F1 address (1), the metrics occurrence recall, occurrence precision, and occurrence F1 address (2), and the measures coverage and lossless compression address (3).
Contribution
Existing approaches to music structure analysis in MIR tend to focus on segmentation (e.g., Weiss & Bello, 2010). The contribution of this task is to afford access to the note content itself (please see the example in Fig. 1A), requiring algorithms to do more than label time windows (e.g., the segmentations in Figs. 1B-D). For instance, a discovery algorithm applied to the piece in Fig. 1A should return a pattern corresponding to the note content of and , as well as a pattern corresponding to the note content of . This is because occurs again independently of the accompaniment in bars 19-22 (not shown here). The ground truth also contains nested patterns, such as in Fig. 1A being a subset of the sectional repetition , reflecting the often-hierarchical nature of musical repetition. While we recognise the appealing simplicity of linear segmentation, in the Discovery of Repeated Themes & Sections task we are demanding analysis at a greater level of detail, and have built a ground truth that contains overlapping and nested patterns (Collins et al., 2014).
Figure 1. Pattern discovery v segmentation. (A) Bars 1-12 of Mozart’s Piano Sonata in E-flat major K282 mvt.2, showing some ground-truth themes and repeated sections; (B-D) Three linear segmentations. Numbers below the staff in Fig. 1A and below the segmentation in Fig. 1D indicate crotchet beats, from zero for bar 1 beat 1.
For a more detailed introduction to the task, please see 2017:Discovery_of_Repeated_Themes_&_Sections.
Ground Truth and Algorithms
The ground truth, called the Johannes Kepler University Patterns Test Database (JKUPTD-Aug2013), is based on motifs and themes in Barlow and Morgenstern (1953), Schoenberg (1967), and Bruhn (1993). Repeated sections are based on those marked by the composer. These annotations are supplemented with some of our own where necessary. A Development Database (JKUPDD-Aug2013) enabled participants to try out their algorithms. For each piece in the Development and Test Databases, symbolic and synthesised audio versions are crossed with monophonic and polyphonic versions, giving four versions of the task in total: symPoly, symMono, audPoly, and audMono. There were no submissions to the audPoly or audMono categories this year, so two versions of the task ran. Submitted algorithms are shown in Table 1.
| Sub code | Submission name | Abstract | Contributors |
|---|---|---|---|
| Task Version | symMono | ||
| CS3 | FindThemeAndSection_Mono | [ Tsung-Ping Chen] | |
| VM1'14 | VM1 | Gissel Velarde, David Meredith | |
| Task Version | symPoly | ||
| CS7 | FindThemeAndSection_Poly | [ Tsung-Ping Chen] |
Table 1. Algorithms submitted to DRTS.
To compare these algorithms to the results or previous years, results of the representative versions of algorithms submitted for symbolic pattern discovery in the previous years are presented as well. The following table shows which algorithms are compared against the new submissions.
| Sub code | Submission name | Abstract | Contributors |
|---|---|---|---|
| Task Version | symMono | ||
| DM1 | SIATECCompress-TLF1 | David Meredith | |
| DM2 | SIATECCompress-TLP | David Meredith | |
| DM3 | SIATECCompress-TLR | David Meredith | |
| NF1 | MotivesExtractor | Oriol Nieto, Morwaread Farbood | |
| OL1'14 | PatMinr | Olivier Lartillot | |
| PLM1 | SYMCHM | Matevž Pesek, Urša Medvešek, Aleš Leonardis, Matija Marolt | |
| Task Version | symPoly | ||
| DM1 | SIATECCompress-TLF1 | David Meredith | |
| DM2 | SIATECCompress-TLP | David Meredith | |
| DM3 | SIATECCompress-TLR | David Meredith |
Table 2. Algorithms submitted to DRTS in previous years, evaluated for comparison.
Results
(For mathematical definitions of the various metrics, please see 2017:Discovery_of_Repeated_Themes_&_Sections#Evaluation_Procedure.)
SymMono
SymPoly
Figures
SymMono
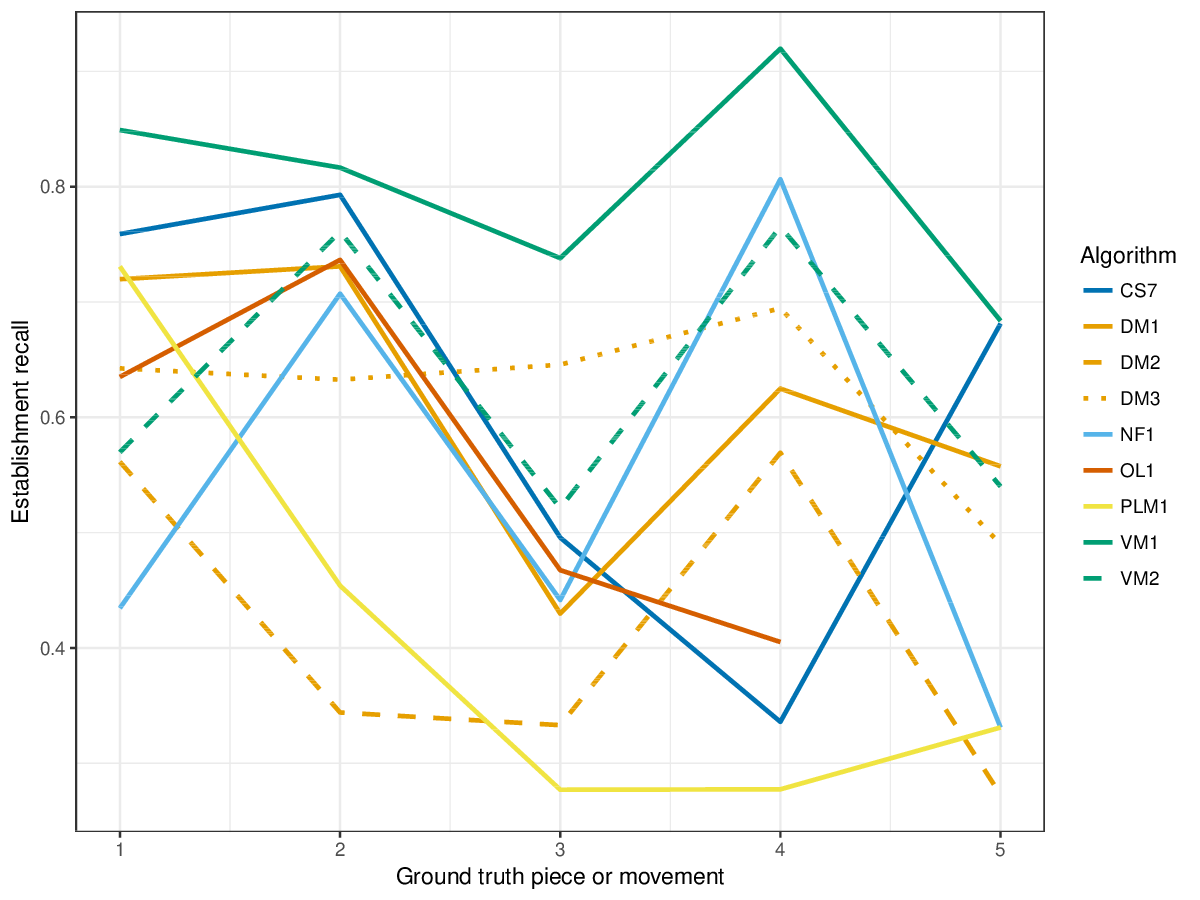
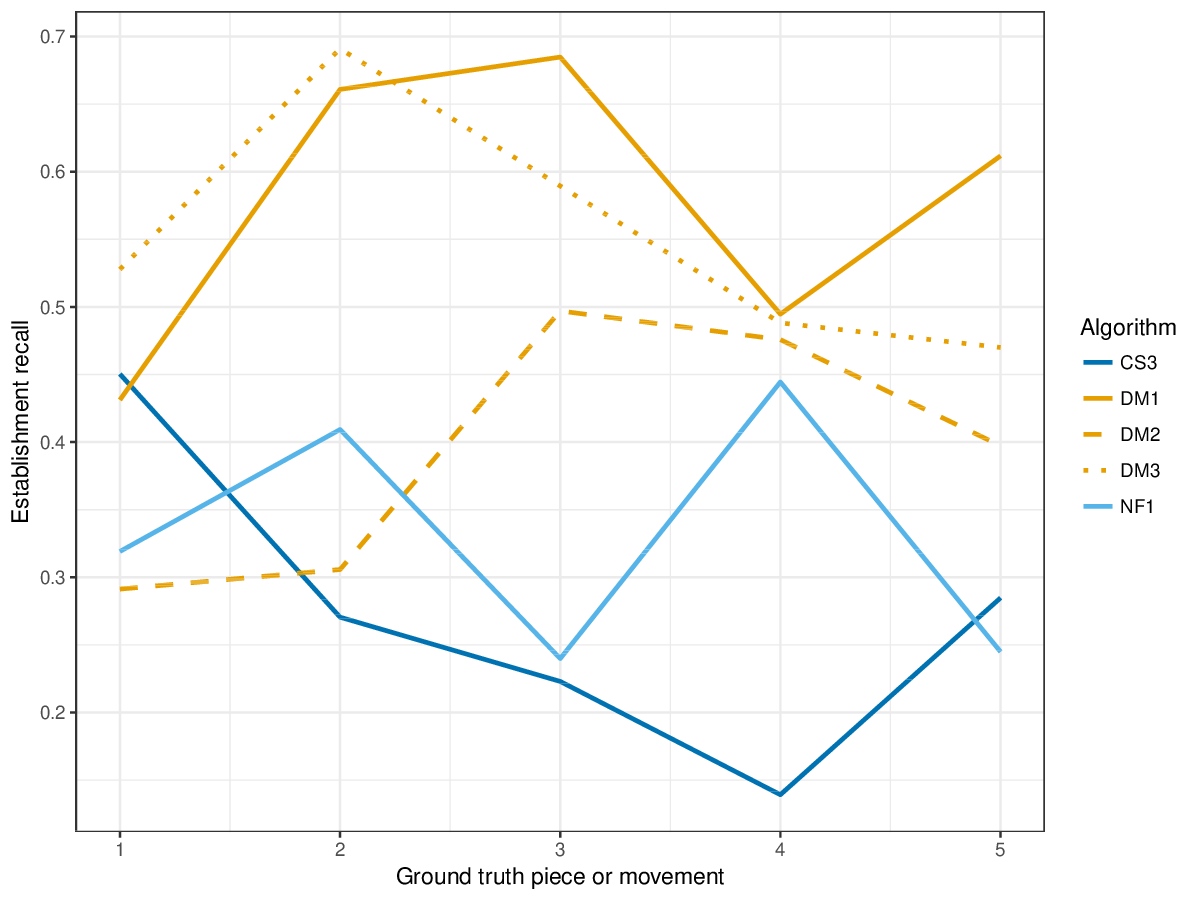
Figure 1. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?
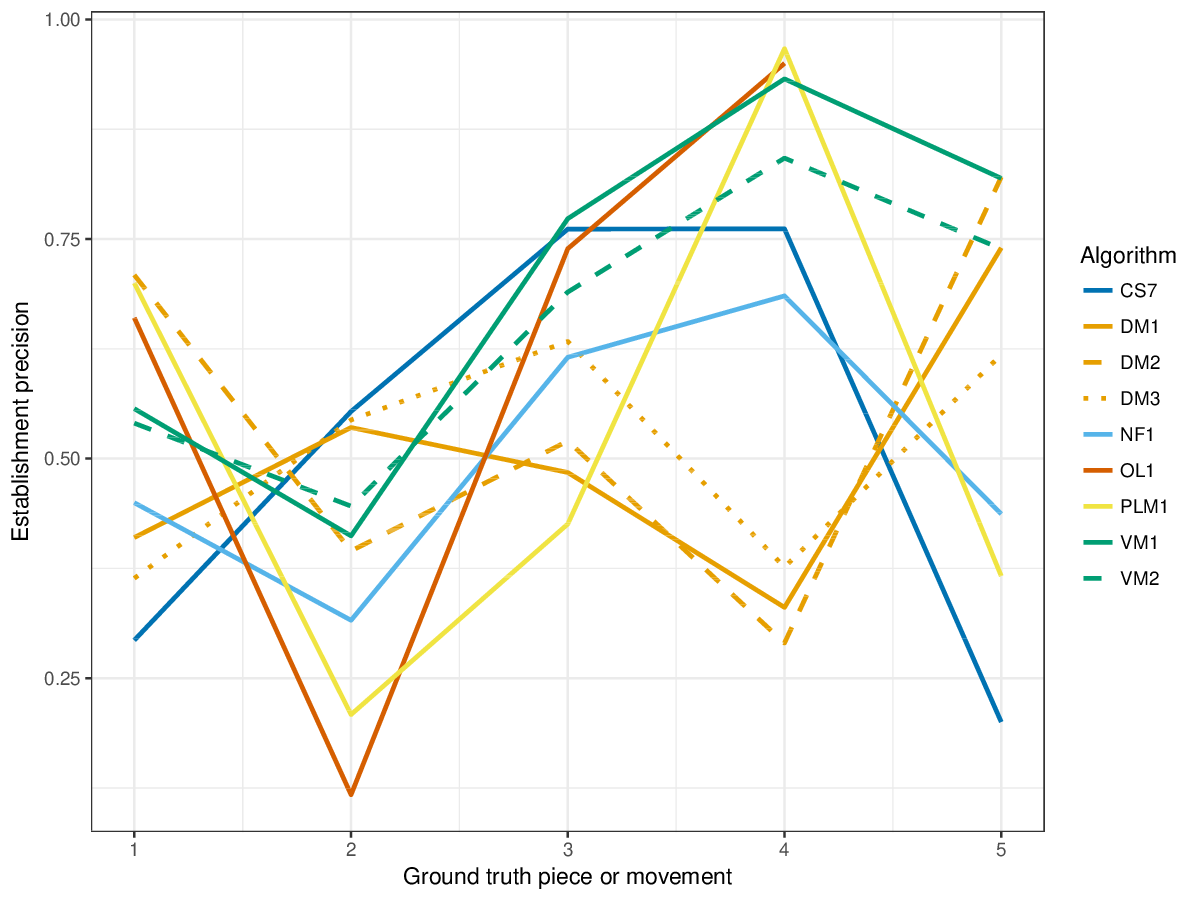
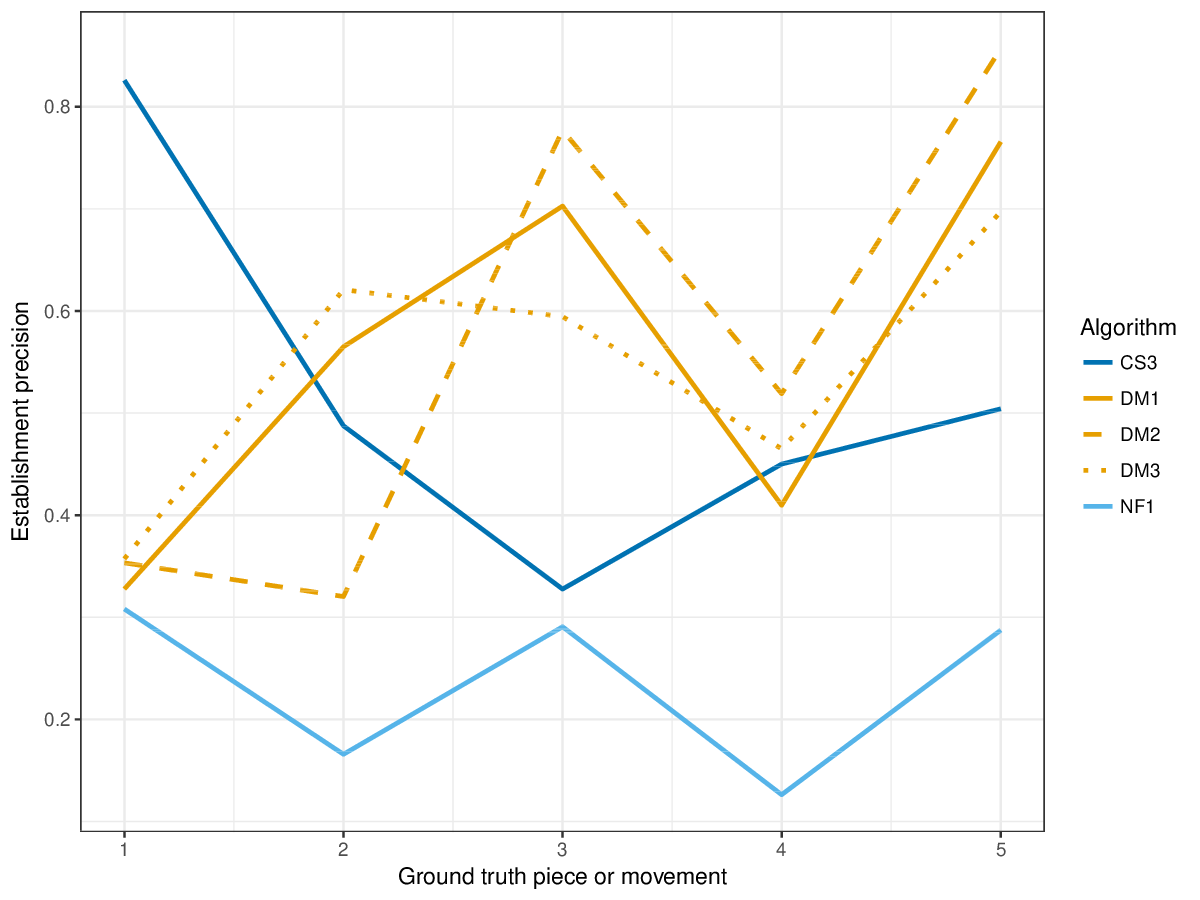
Figure 2. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?
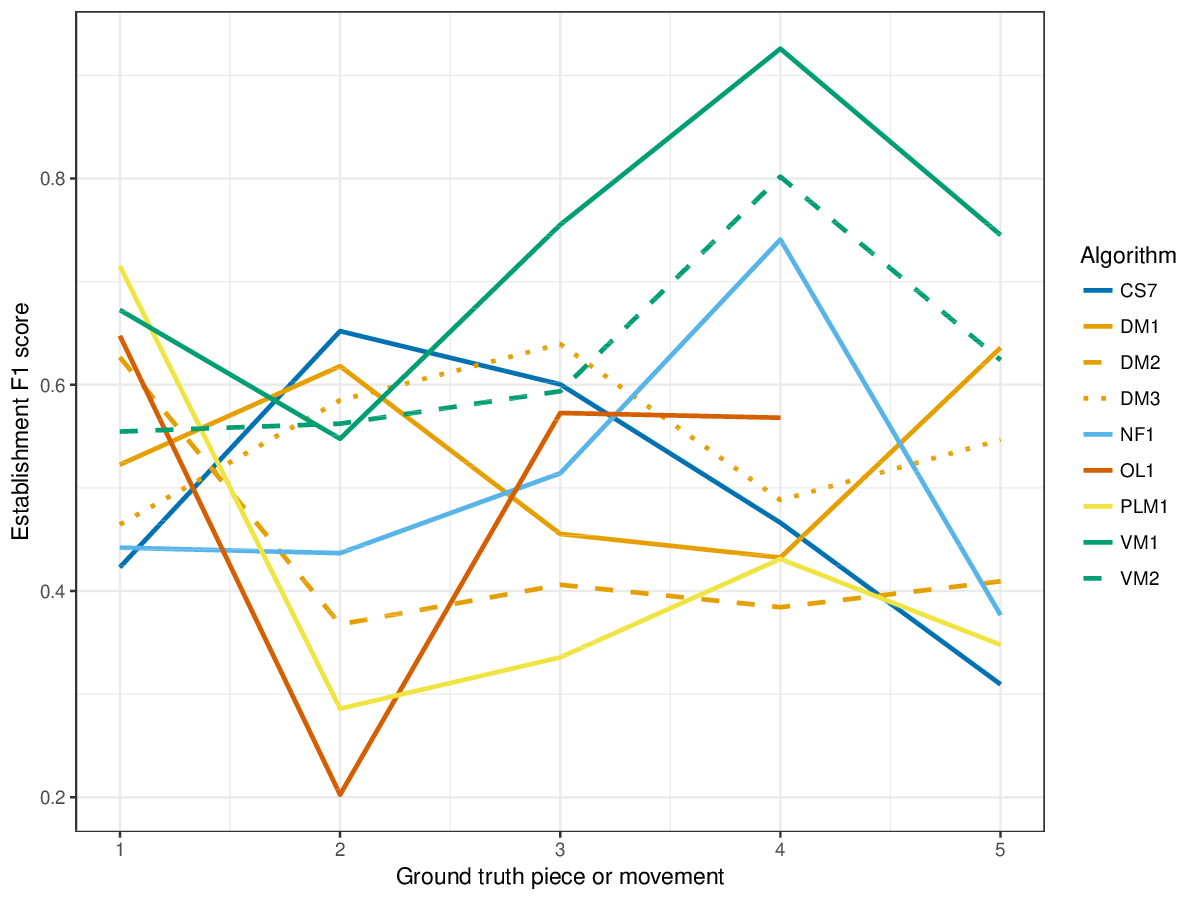
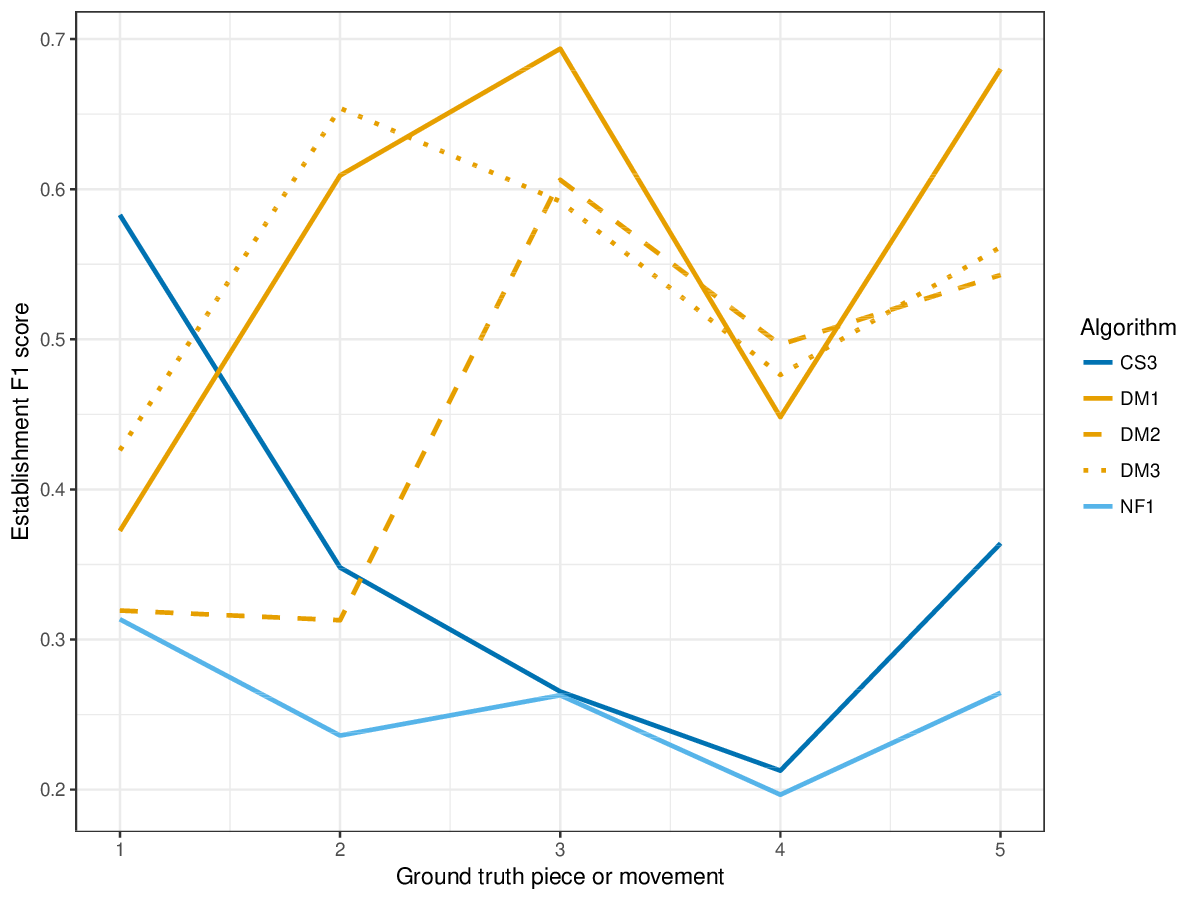
Figure 3. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.
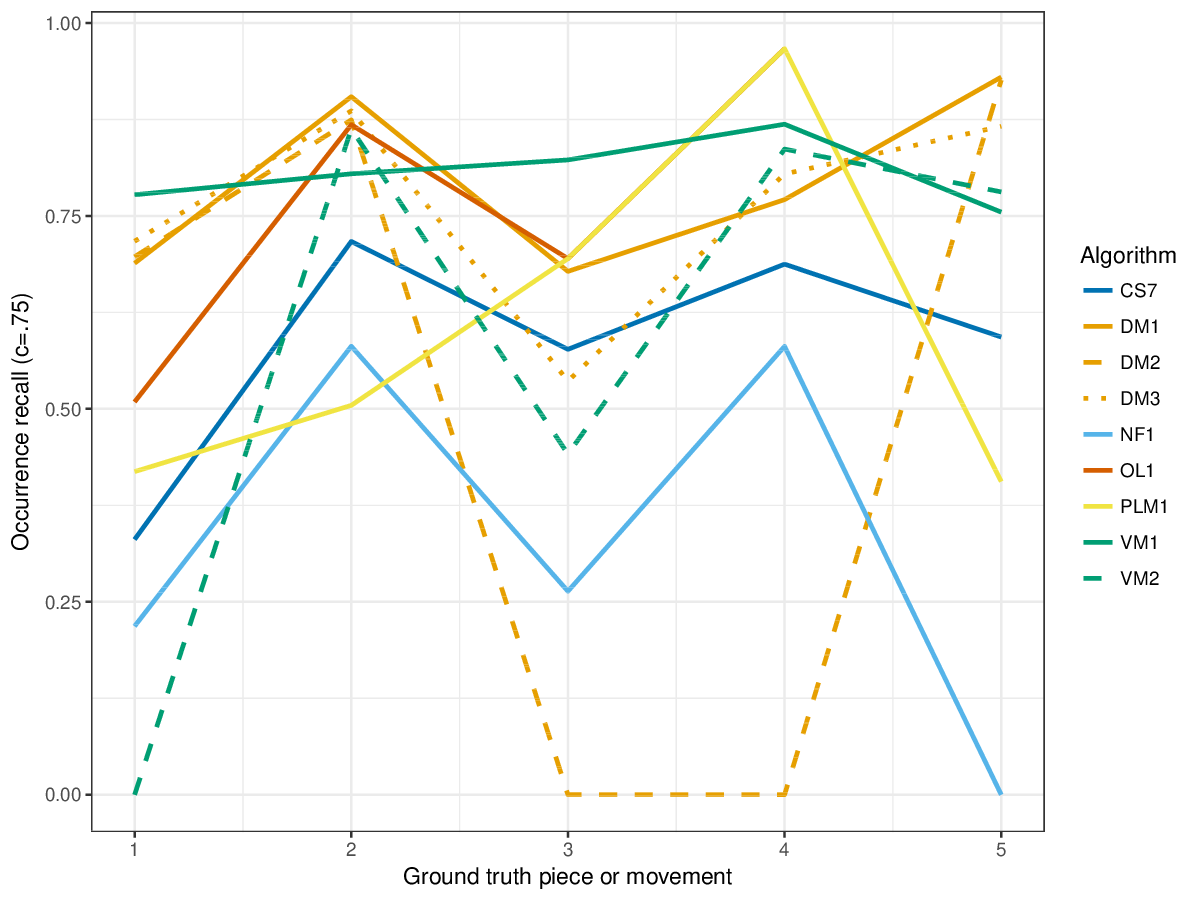
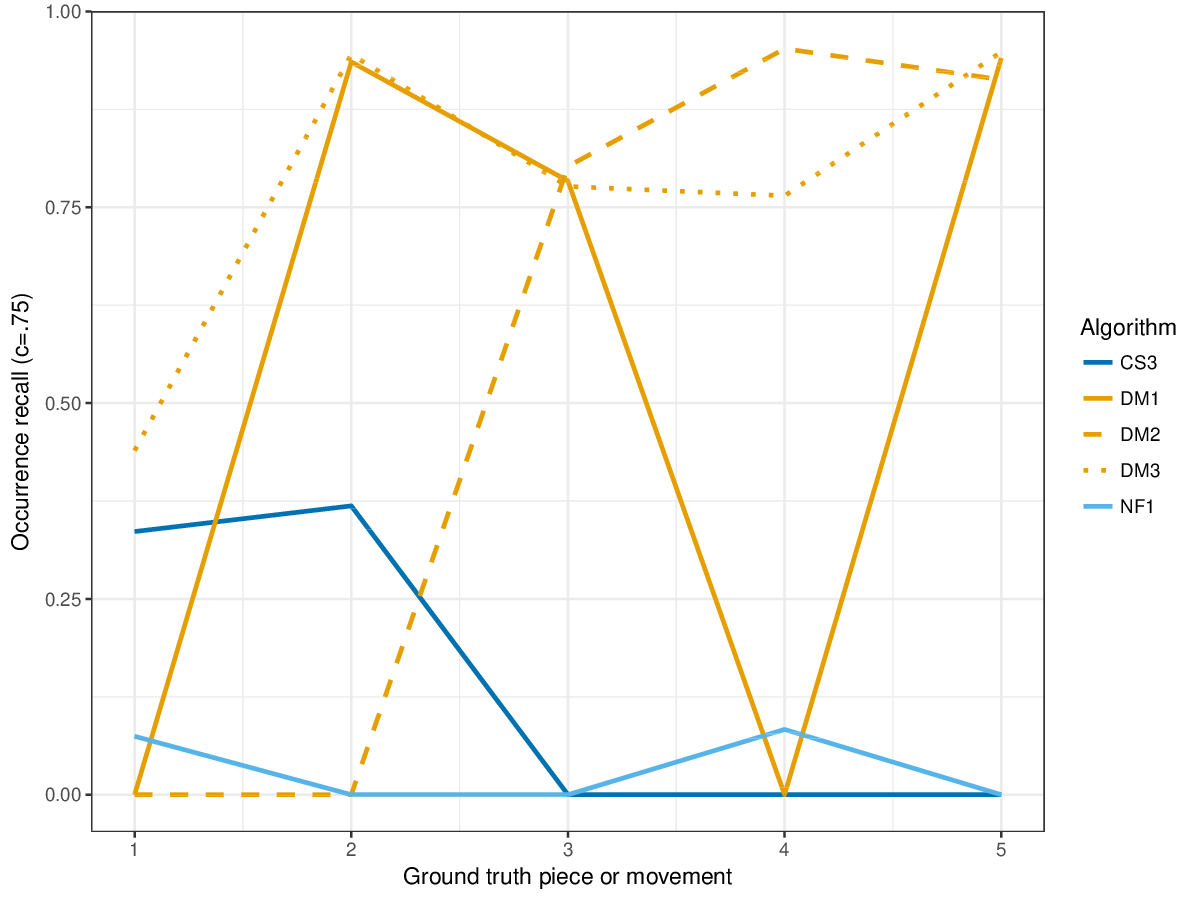
Figure 4. Occurrence recall () averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?
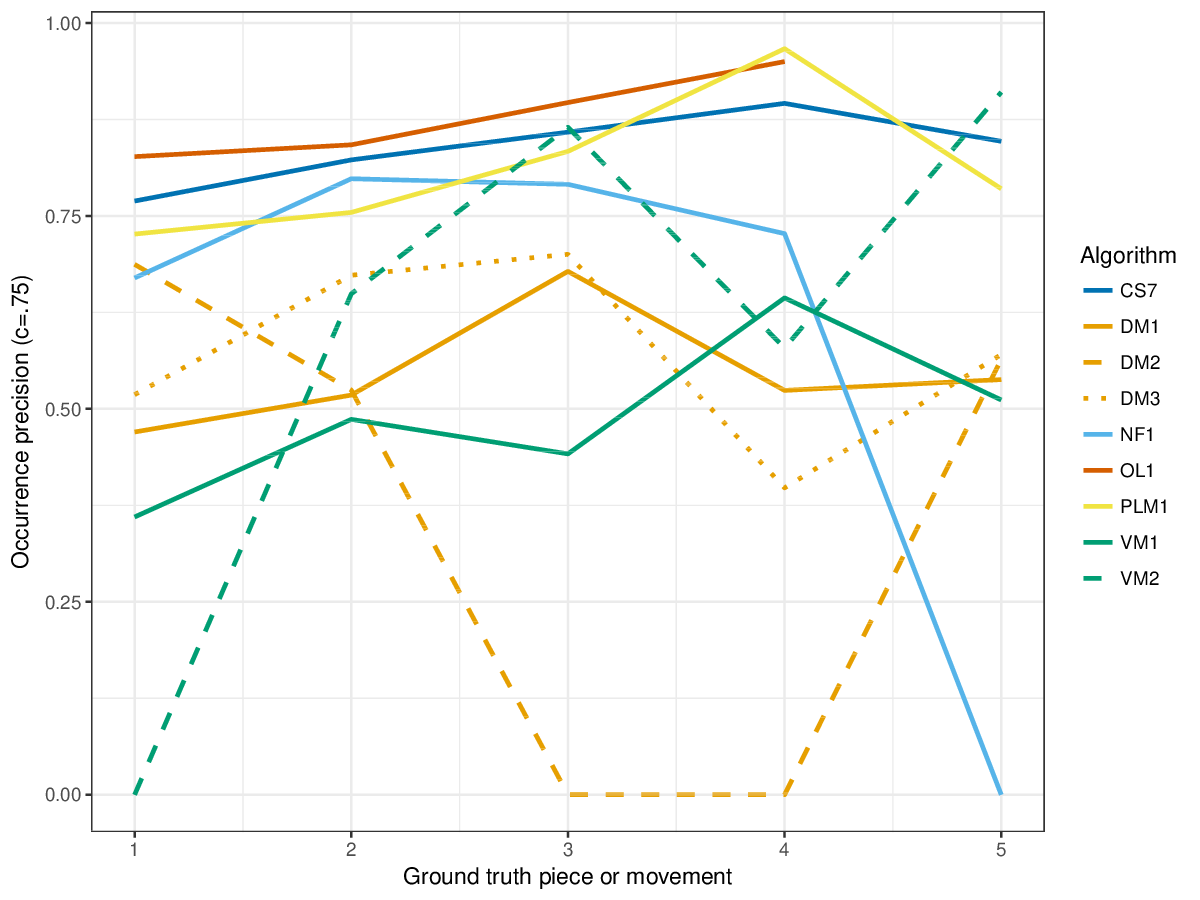
Figure 5. Occurrence precision () averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?
Figure 6. Occurrence F1 () averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.
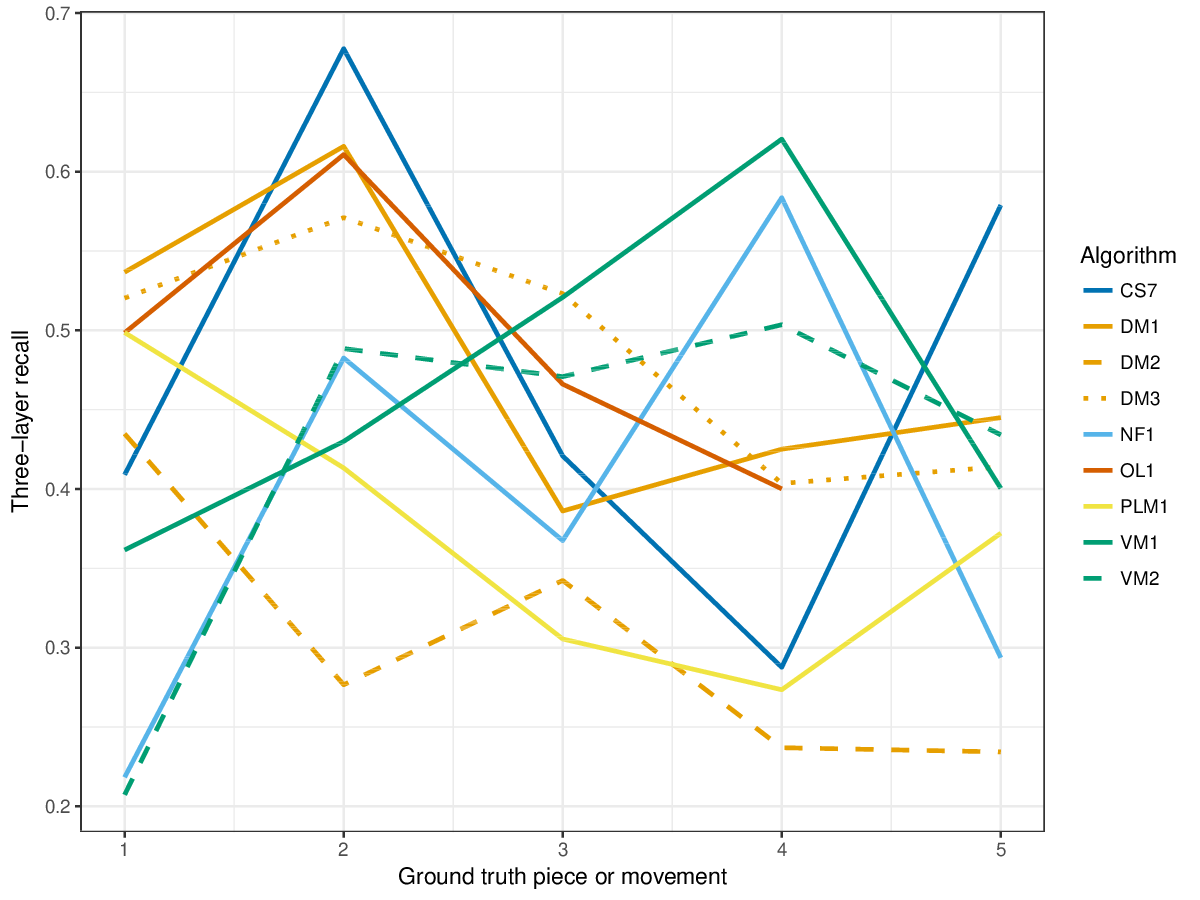
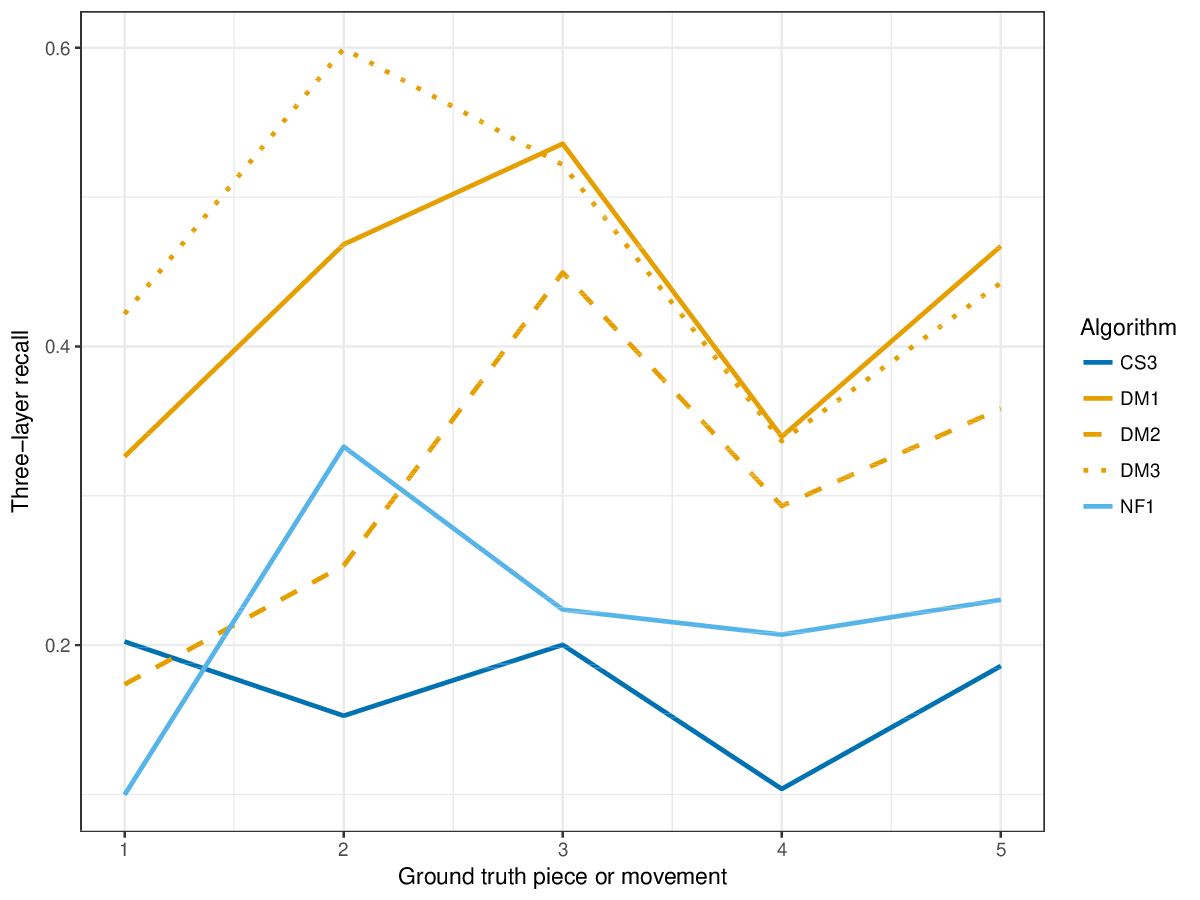
Figure 7. Three-layer recall averaged over each piece/movement. Rather than using as a similarity measure (which is the default for establishment recall), three-layer recall uses , which is a kind of F1 measure.
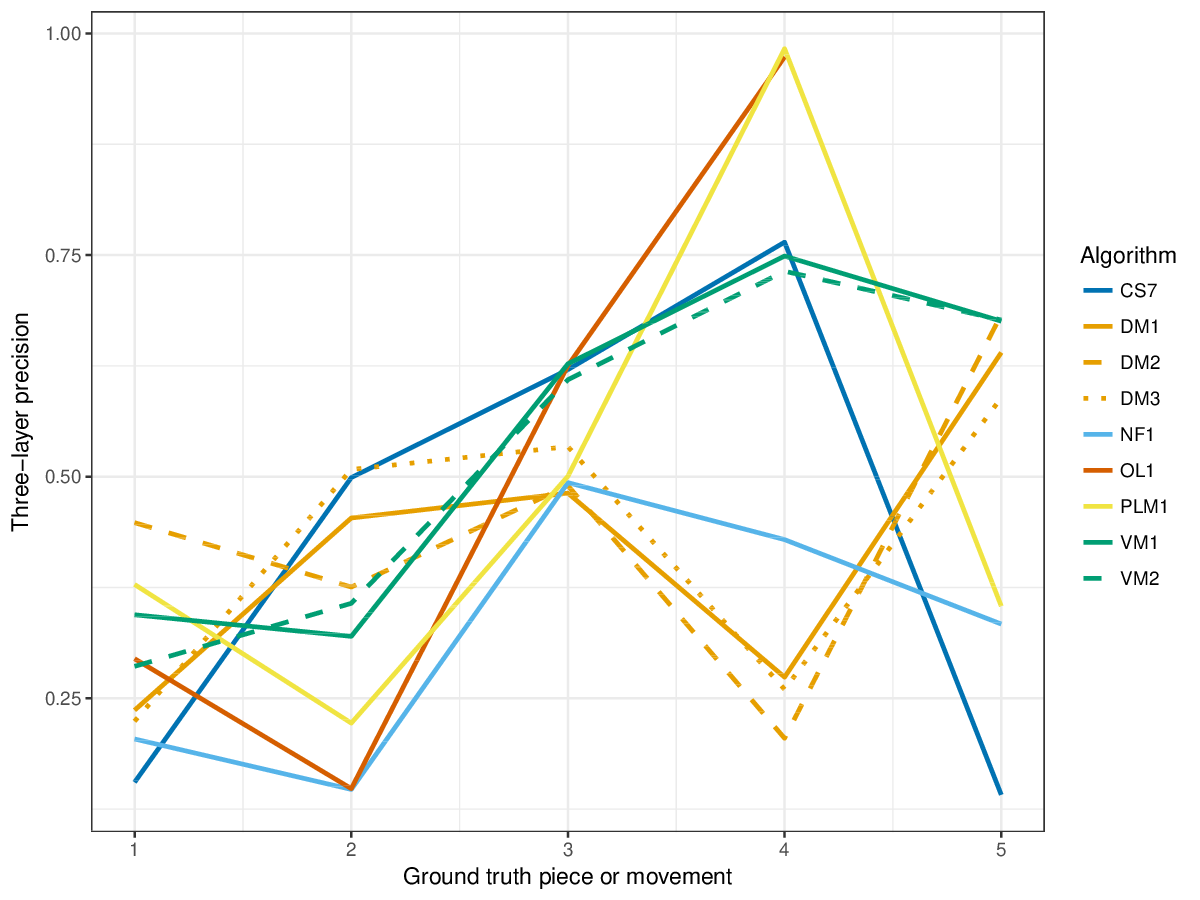
Figure 8. Three-layer precision averaged over each piece/movement. Rather than using as a similarity measure (which is the default for establishment precision), three-layer precision uses , which is a kind of F1 measure.
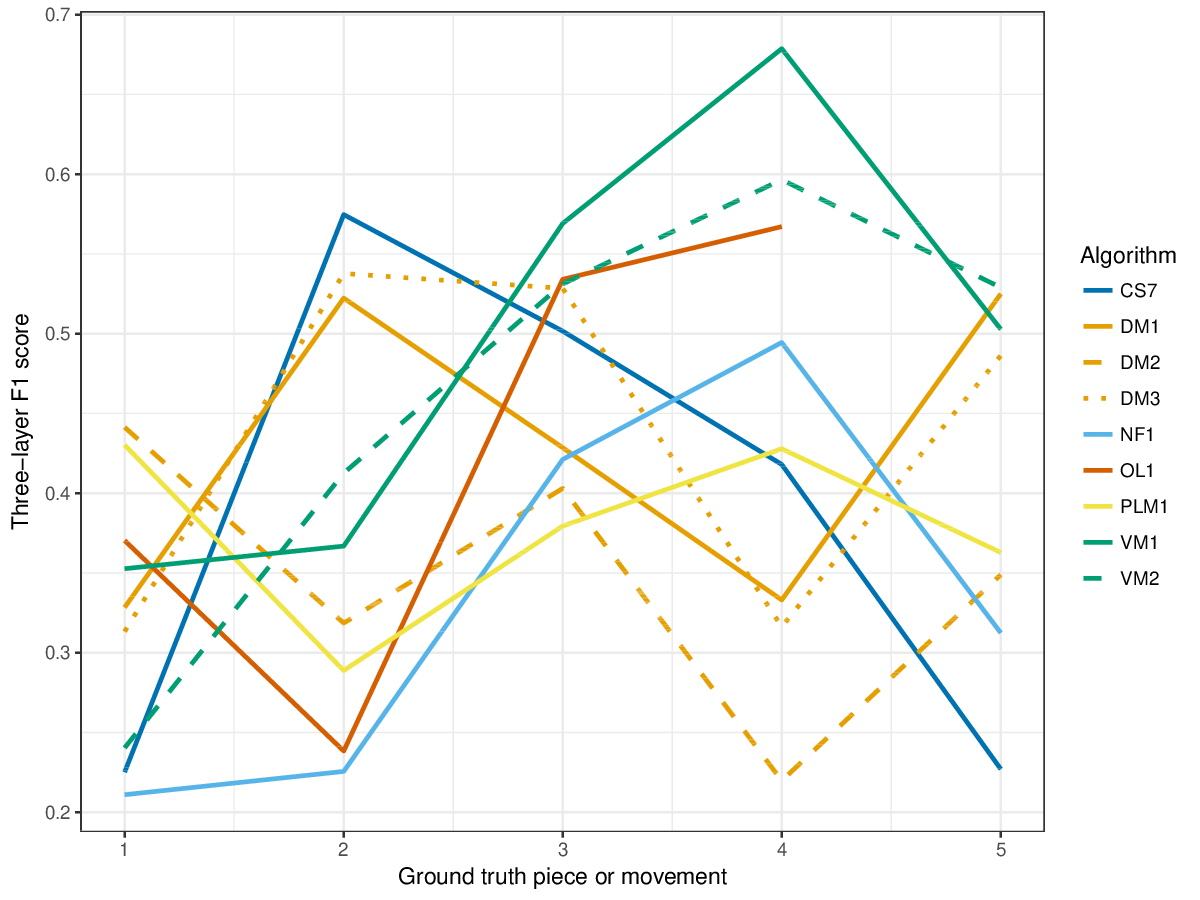
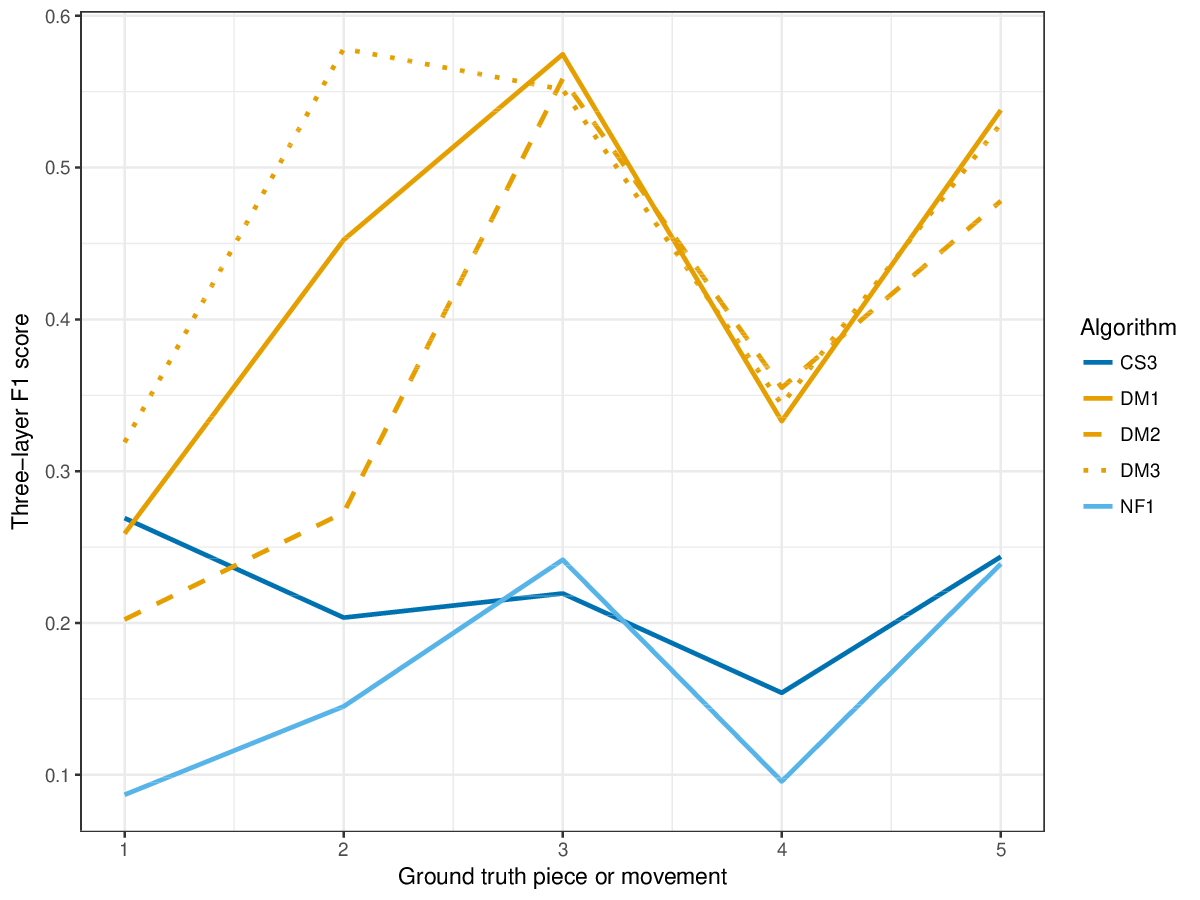
Figure 9. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.
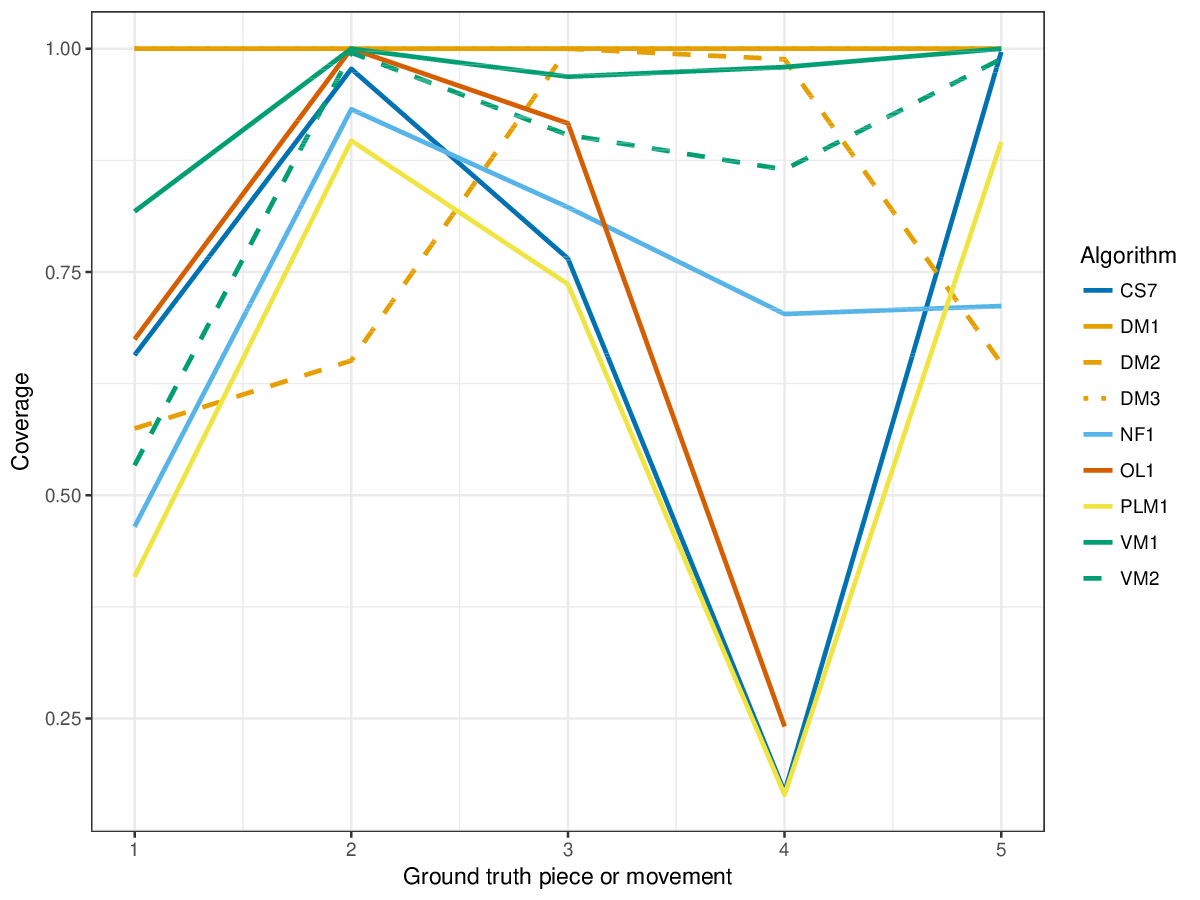
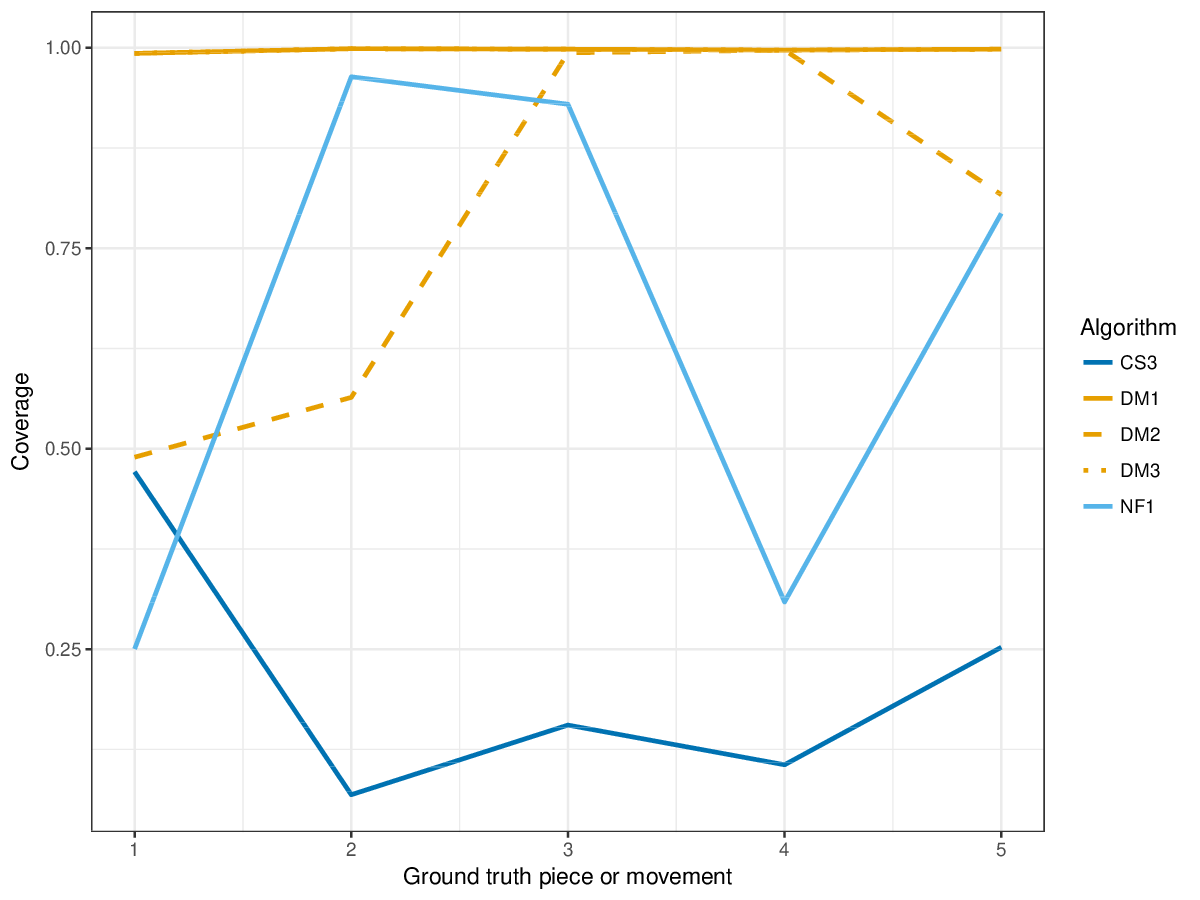
Figure 10. Coverage of the discovered patterns of each piece/movement. Coverage measures the fraction of notes of a piece covered by discovered patterns.
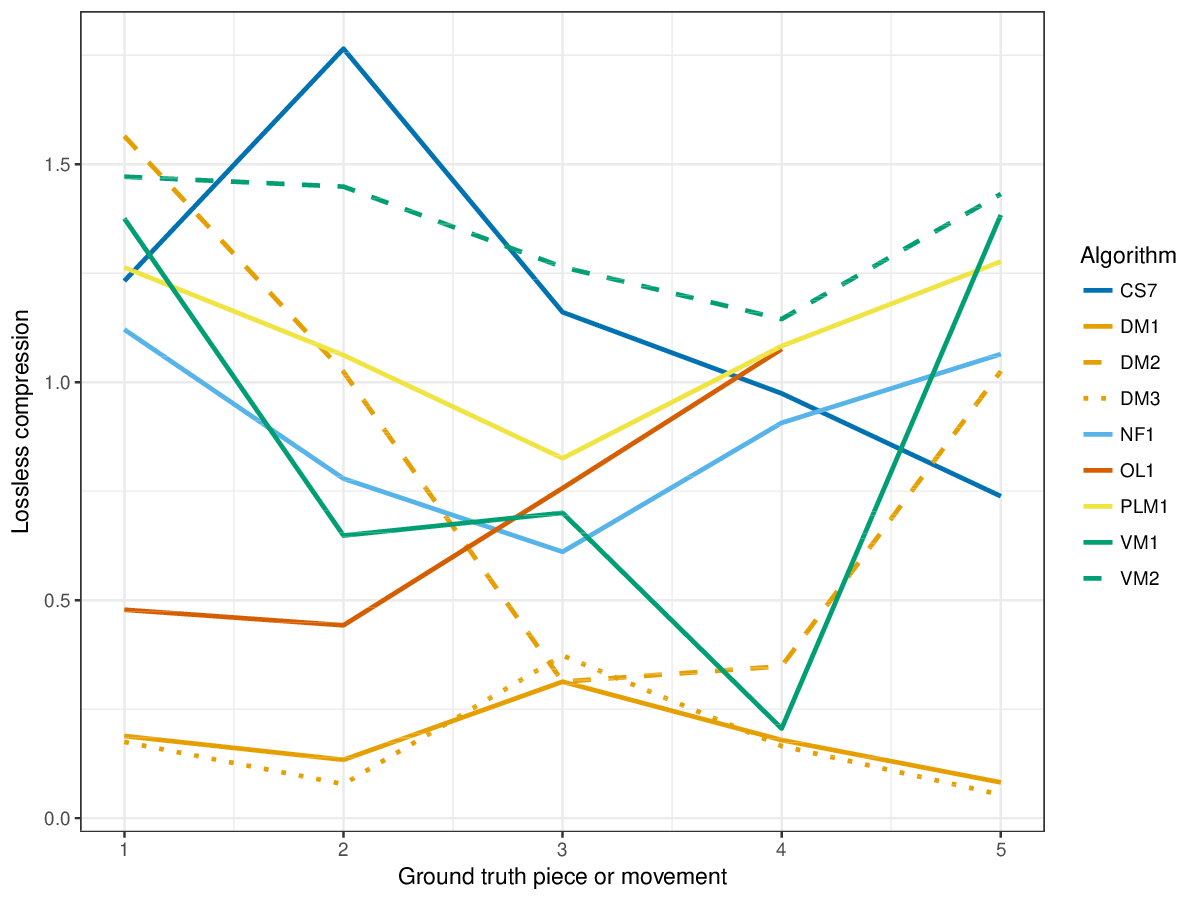
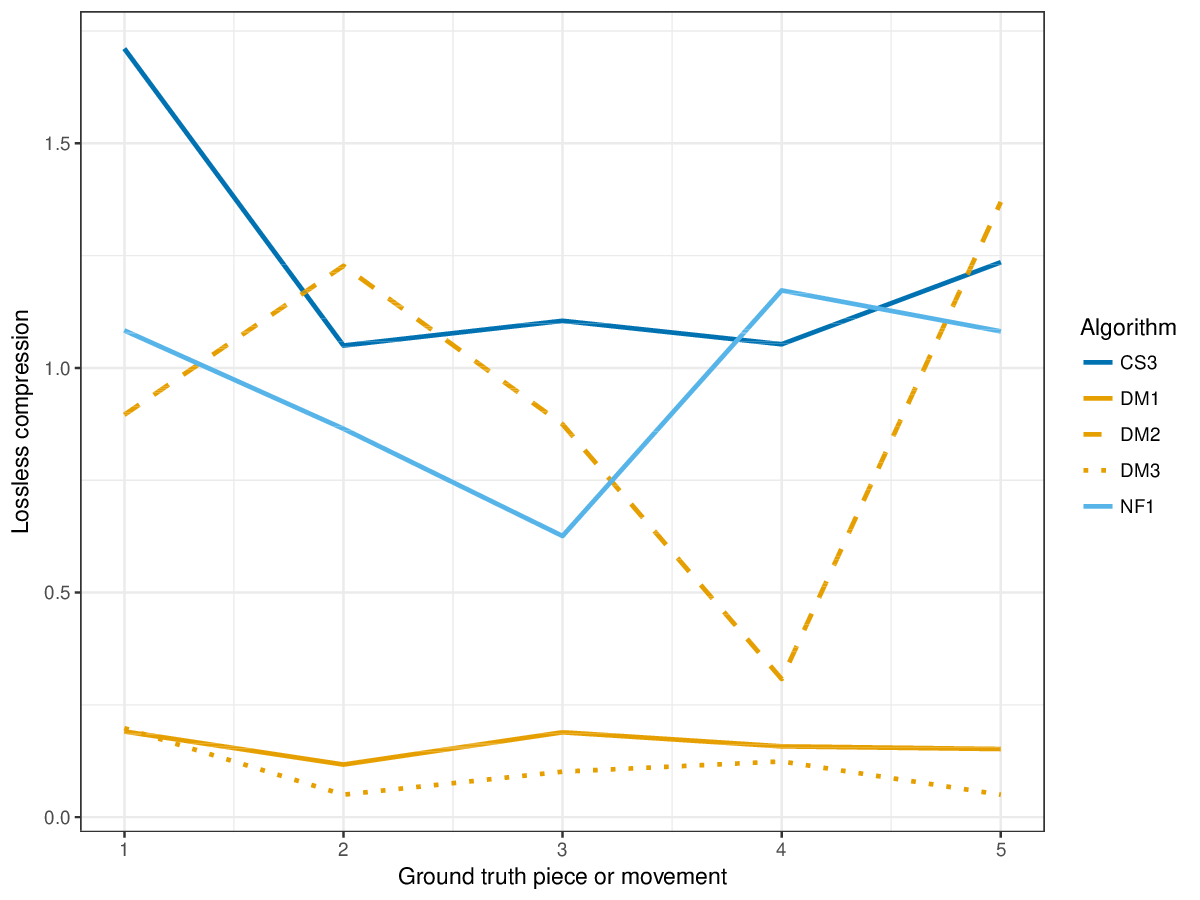
Figure 11. Lossless compression achieved by representing each piece/movement in terms of patterns discovered by a given algorithm. Next to patterns and their repetitions, also the uncovered notes are represented, such that the complete piece could be reconstructed from the compressed representation.
SymPoly
Figure 12. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?
Figure 13. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?
Figure 14. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.
Figure 15. Occurrence recall () averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?
Figure 16. Occurrence precision () averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?
Figure 17. Occurrence F1 () averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.
Figure 18. Three-layer recall averaged over each piece/movement. Rather than using as a similarity measure (which is the default for establishment recall), three-layer recall uses , which is a kind of F1 measure.
Figure 19. Three-layer precision averaged over each piece/movement. Rather than using as a similarity measure (which is the default for establishment precision), three-layer precision uses , which is a kind of F1 measure.
Figure 20. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.
Figure 21. Coverage of the discovered patterns of each piece/movement. Coverage measures the fraction of notes of a piece covered by discovered patterns.
Figure 22. Lossless compression achieved by representing each piece/movement in terms of patterns discovered by a given algorithm. Next to patterns and their repetitions, also the uncovered notes are represented, such that the complete piece could be reconstructed from the compressed representation.