Difference between revisions of "2017:Discovery of Repeated Themes & Sections Results"
(→Introduction) |
(→Ground Truth and Algorithms) |
||
| Line 39: | Line 39: | ||
! | ! | ||
|- | |- | ||
| − | ! | + | ! CS7 |
| − | | FindThemeAndSection_Poly || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2017/ | + | | FindThemeAndSection_Poly || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2017/CS7.pdf PDF] || [ Tsung-Ping Chen] |
|- | |- | ||
|- style="background: green;" | |- style="background: green;" | ||
| Line 48: | Line 48: | ||
! | ! | ||
|- | |- | ||
| − | ! | + | ! CS3 |
| − | | FindThemeAndSection_Mono || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2017/ | + | | FindThemeAndSection_Mono || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2017/CS3.pdf PDF] || [ Tsung-Ping Chen] |
|- | |- | ||
! VM1'14 | ! VM1'14 | ||
| Line 57: | Line 57: | ||
'''Table 1.''' Algorithms submitted to DRTS. | '''Table 1.''' Algorithms submitted to DRTS. | ||
| + | |||
| + | To compare these algorithms to the results or previous years, results of the representative versions of algorithms submitted in the previous years are presented as well. The following table shows which algorithms are compared against the new submissions. | ||
| + | |||
| + | {| border="1" cellspacing="0" style="text-align: left; width: 800px;" | ||
| + | |- style="background: yellow;" | ||
| + | ! width="80" | Sub code | ||
| + | ! width="200" | Submission name | ||
| + | ! width="80" style="text-align: center;" | Abstract | ||
| + | ! width="440" | Contributors | ||
| + | |- | ||
| + | |- style="background: green;" | ||
| + | ! Task Version | ||
| + | ! symPoly | ||
| + | ! | ||
| + | ! | ||
| + | |- | ||
| + | ! DM1 | ||
| + | | SIATECCompress-TLF1 || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2016/DM1.pdf PDF] || [http://www.titanmusic.com/ David Meredith] | ||
| + | |- | ||
| + | ! DM2 | ||
| + | | SIATECCompress-TLP || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2016/DM2.pdf PDF] || [http://www.titanmusic.com/ David Meredith] | ||
| + | |- | ||
| + | ! DM3 | ||
| + | | SIATECCompress-TLR || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2016/DM3.pdf PDF] || [http://www.titanmusic.com/ David Meredith] | ||
| + | |- | ||
| + | |- | ||
| + | ! OL1'14 | ||
| + | | PatMinr || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2014/OL1.pdf PDF] || [http://scholar.google.com/citations?user=aiYUZV4AAAAJ&hl=da Olivier Lartillot] | ||
| + | ! PLM1 | ||
| + | | SYMCHM || style="text-align: center;" | [https://www.music-ir.org/mirex/abstracts/2016/PLM1.pdf PDF] || [http://musiclab.si/ Matevž Pesek], Urša Medvešek, [http://www.cs.bham.ac.uk/~leonarda/ Aleš Leonardis], [http://www.fri.uni-lj.si/en/matija-marolt Matija Marolt] | ||
== Results == | == Results == | ||
Revision as of 05:26, 14 October 2017
THIS PAGE IS UNDER CONSTRUCTION
Contents
Introduction
The task: algorithms take a piece of music as input, and output a list of patterns repeated within that piece. A pattern is defined as a set of ontime-pitch pairs that occurs at least twice (i.e., is repeated at least once) in a piece of music. The second, third, etc. occurrences of the pattern will likely be shifted in time and/or transposed, relative to the first occurrence. Ideally an algorithm will be able to discover all exact and inexact occurrences of a pattern within a piece, so in evaluating this task we are interested in both:
- (1) to what extent an algorithm can discover one occurrence, up to time shift and transposition;
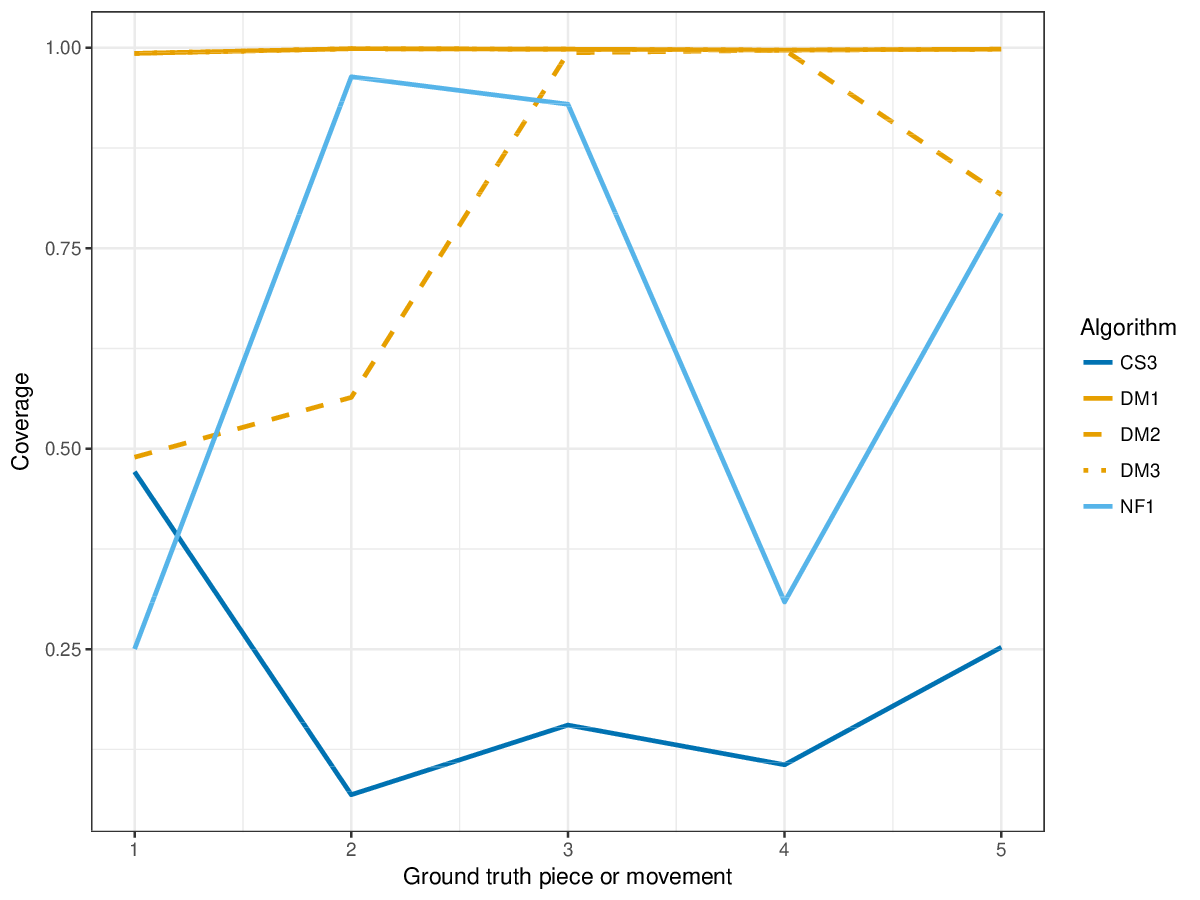
- (2) to what extent it can find all occurrences, and;
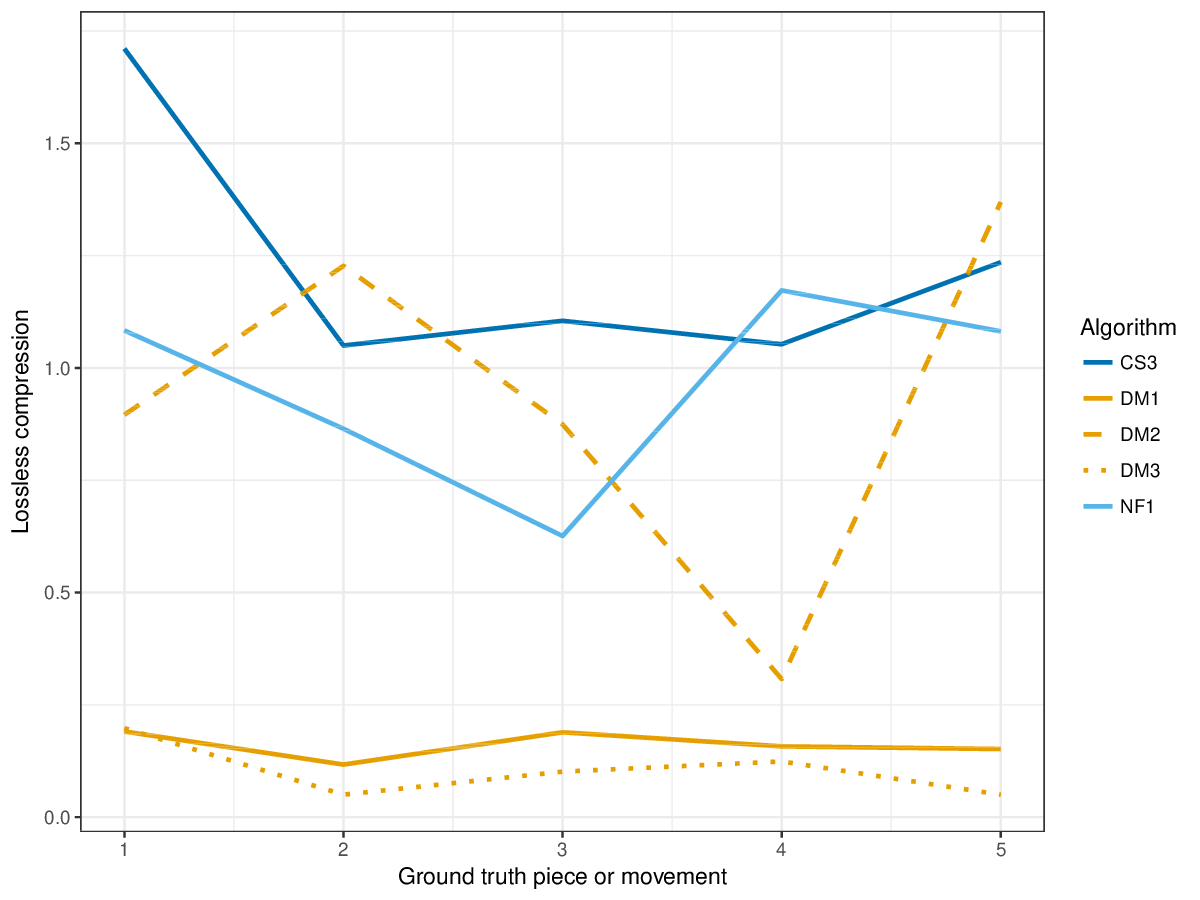
- (3) to what extent repeated patterns discovered by an algorithm allow for compression of a melody.
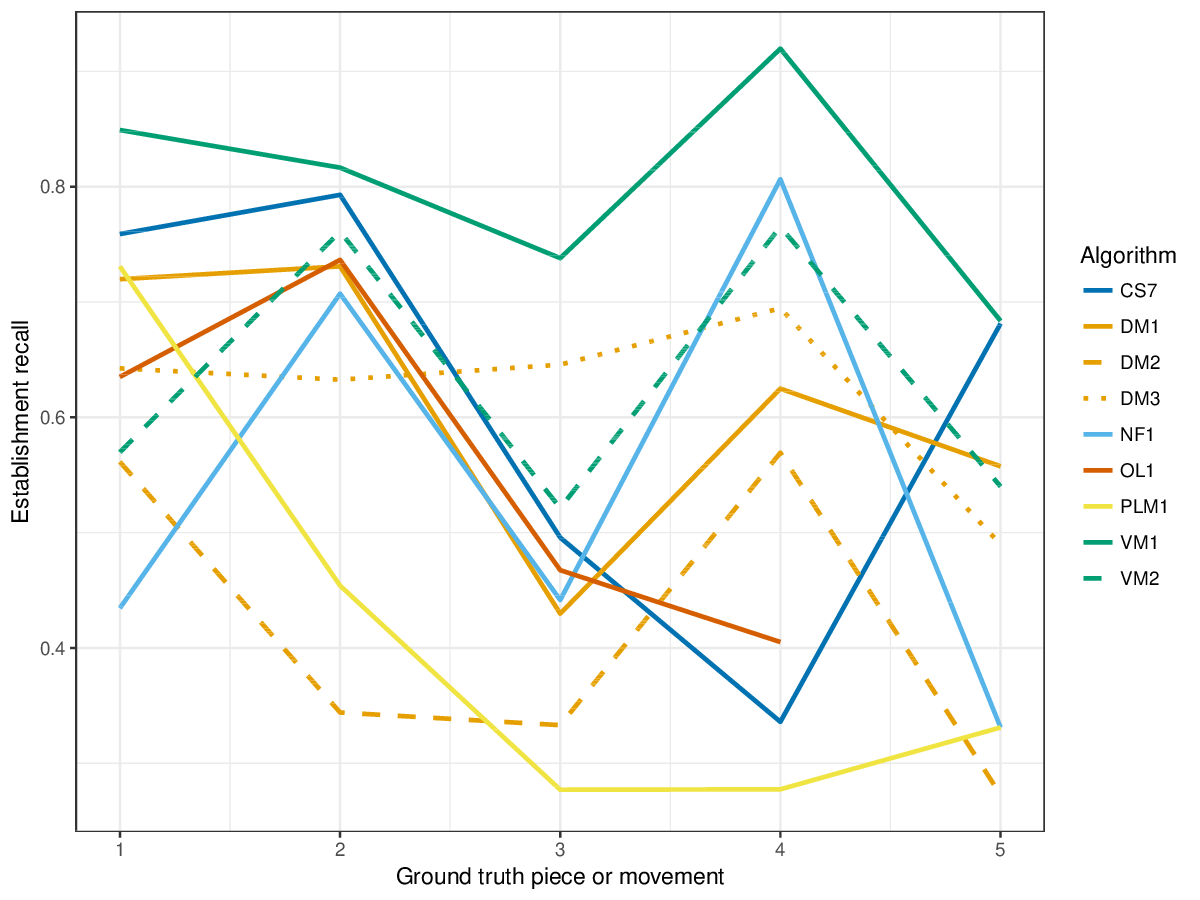
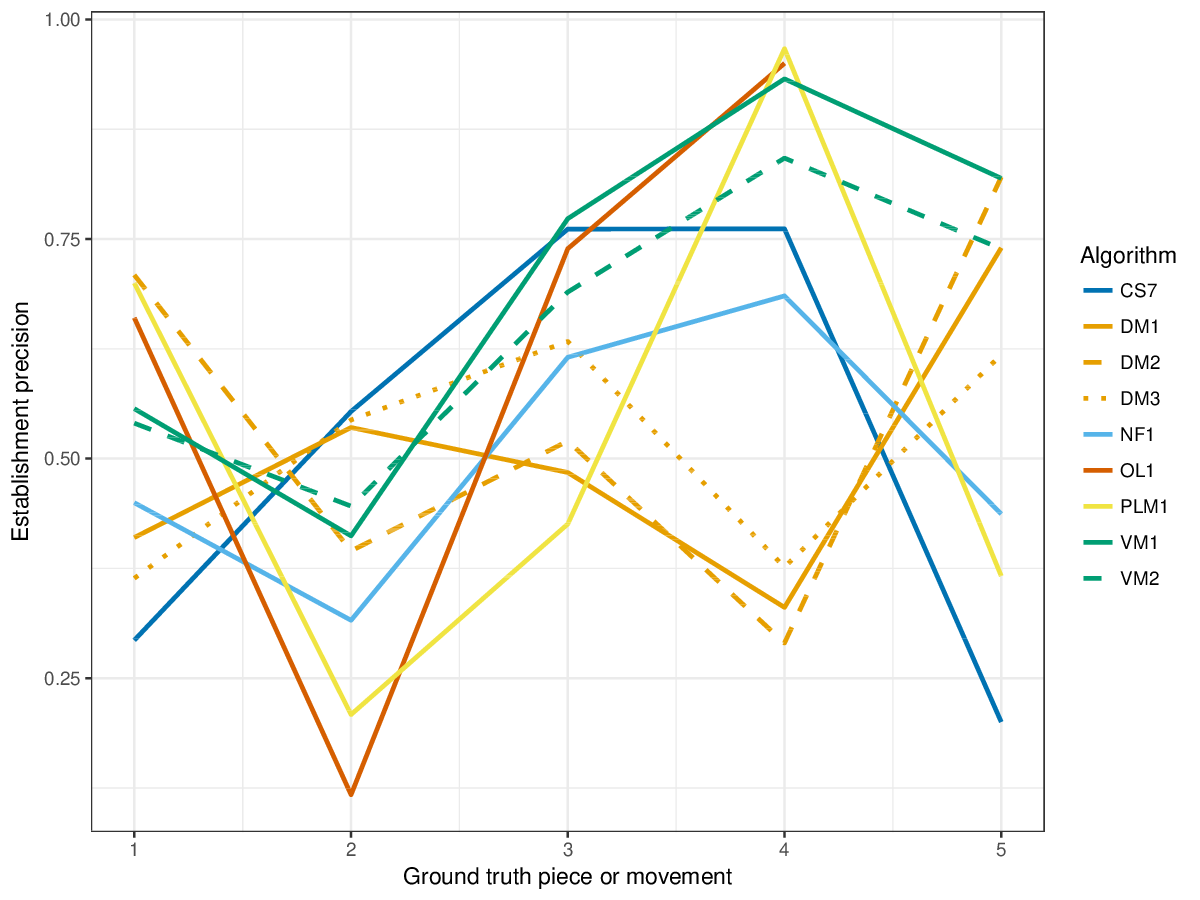
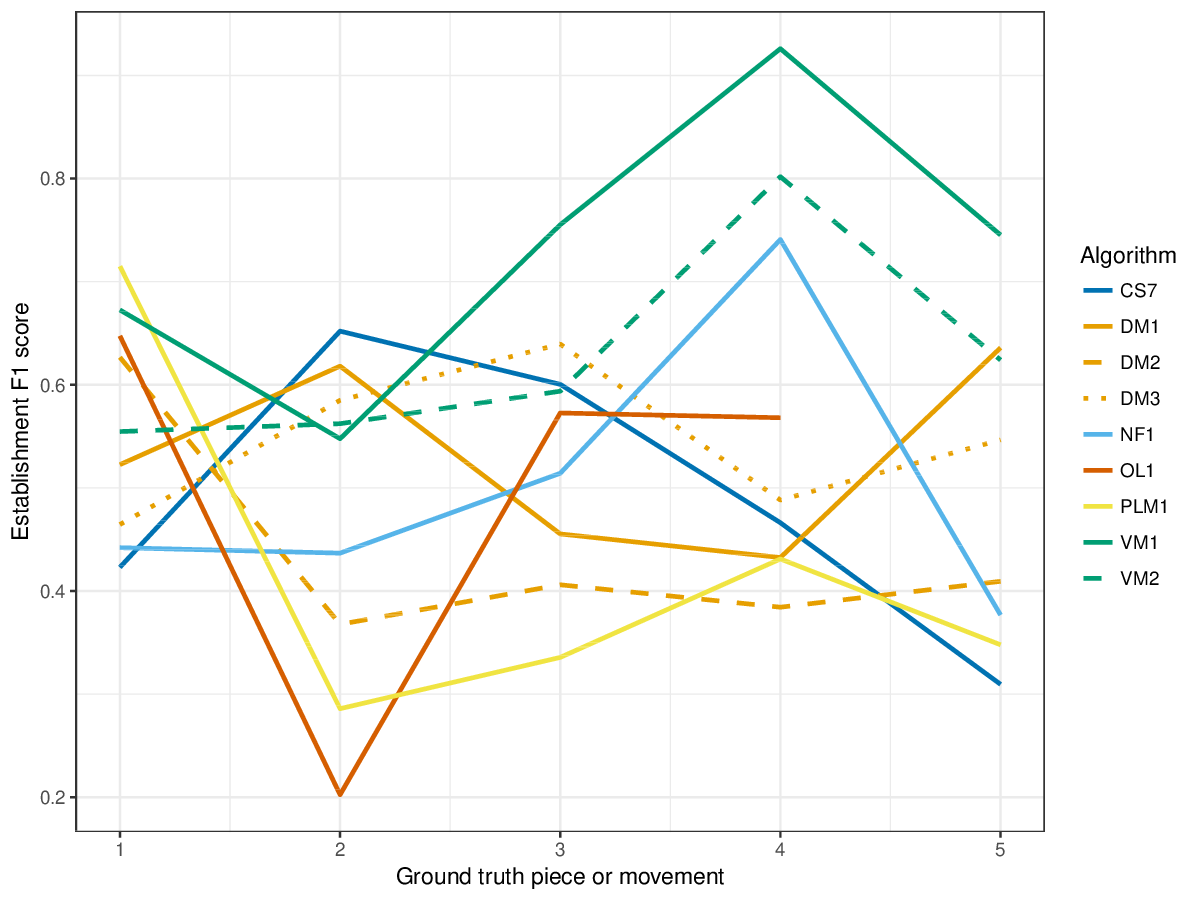
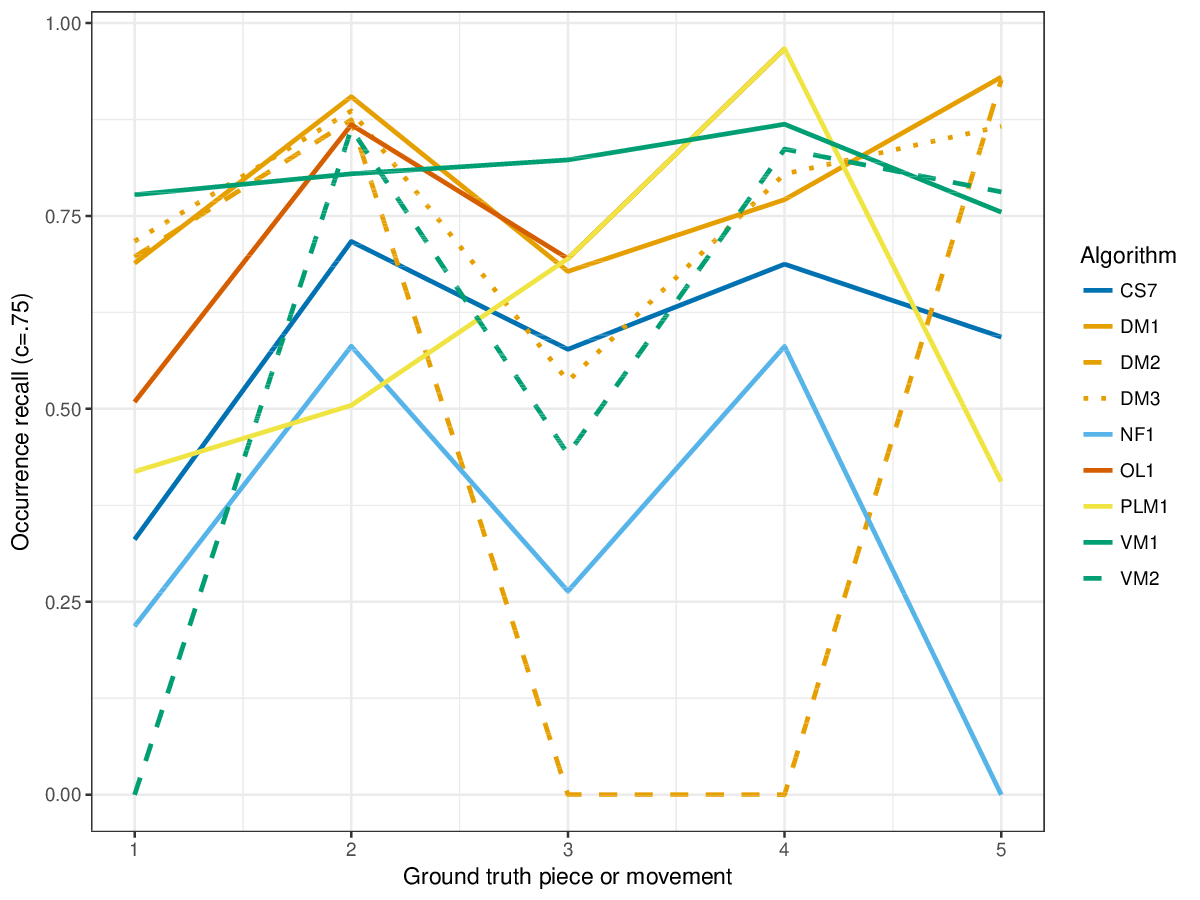
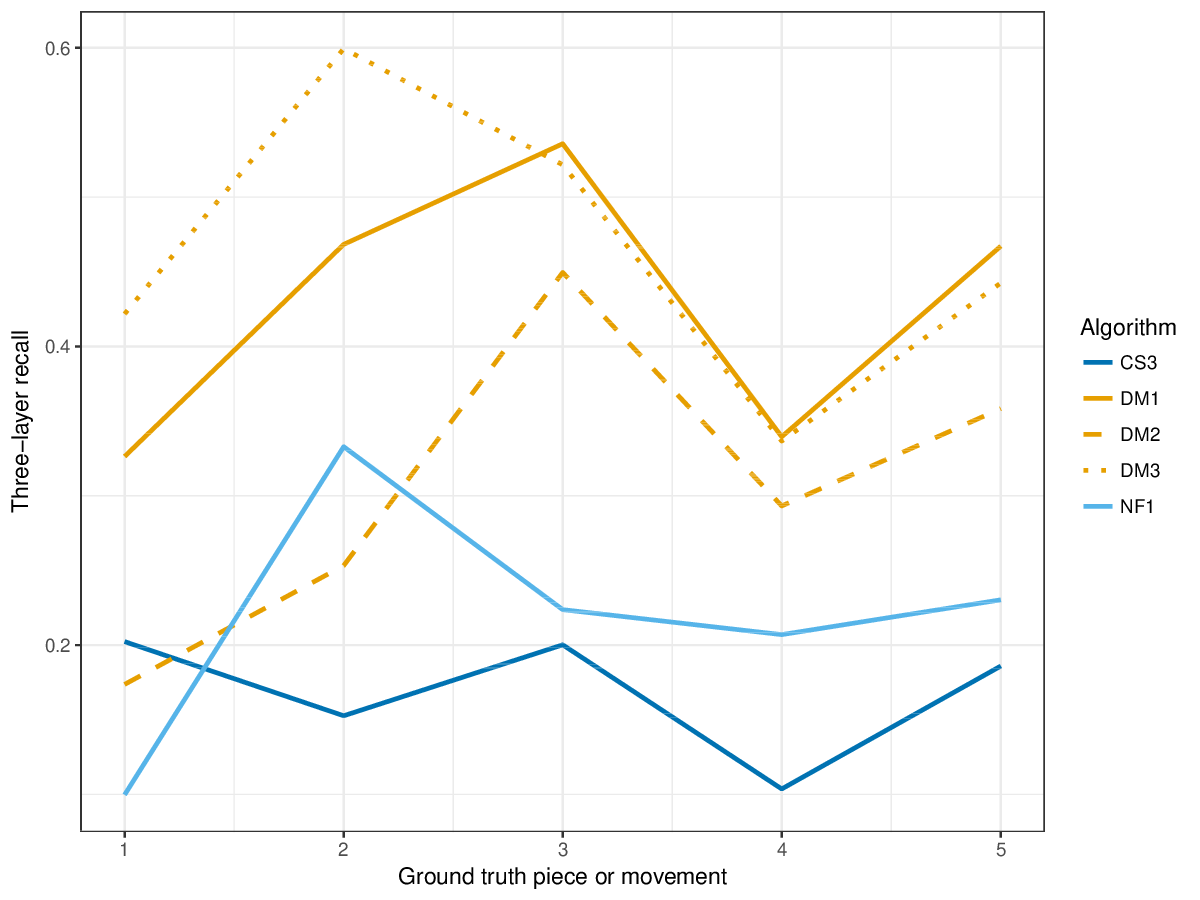
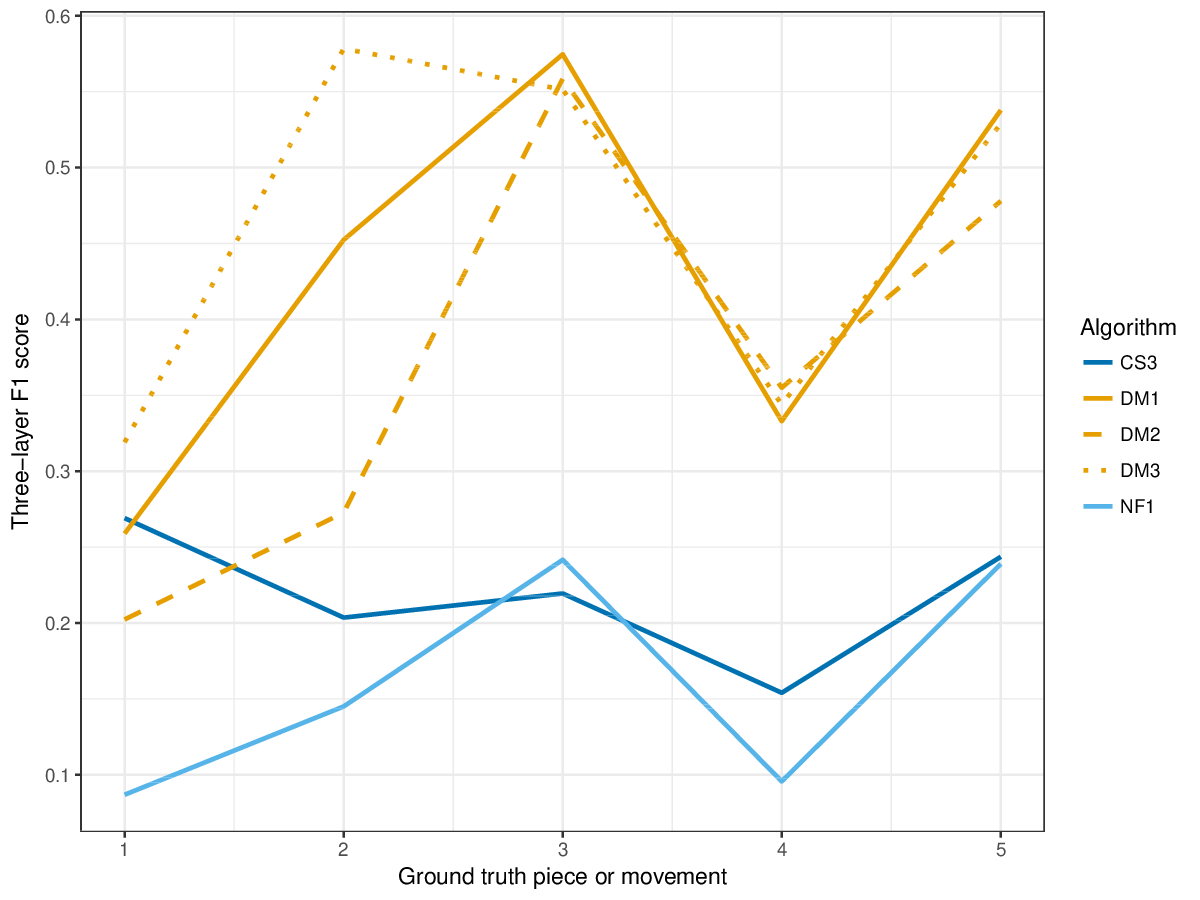
The metrics establishment recall, establishment precision and establishment F1 address (1), and the metrics occurrence recall, occurrence precision, and occurrence F1 address (2).
Contribution
Existing approaches to music structure analysis in MIR tend to focus on segmentation (e.g., Weiss & Bello, 2010). The contribution of this task is to afford access to the note content itself (please see the example in Fig. 1A), requiring algorithms to do more than label time windows (e.g., the segmentations in Figs. 1B-D). For instance, a discovery algorithm applied to the piece in Fig. 1A should return a pattern corresponding to the note content of and , as well as a pattern corresponding to the note content of . This is because occurs again independently of the accompaniment in bars 19-22 (not shown here). The ground truth also contains nested patterns, such as in Fig. 1A being a subset of the sectional repetition , reflecting the often-hierarchical nature of musical repetition. While we recognise the appealing simplicity of linear segmentation, in the Discovery of Repeated Themes & Sections task we are demanding analysis at a greater level of detail, and have built a ground truth that contains overlapping and nested patterns (Collins et al., 2014).
Figure 1. Pattern discovery v segmentation. (A) Bars 1-12 of Mozart’s Piano Sonata in E-flat major K282 mvt.2, showing some ground-truth themes and repeated sections; (B-D) Three linear segmentations. Numbers below the staff in Fig. 1A and below the segmentation in Fig. 1D indicate crotchet beats, from zero for bar 1 beat 1.
For a more detailed introduction to the task, please see 2017:Discovery_of_Repeated_Themes_&_Sections.
Ground Truth and Algorithms
The ground truth, called the Johannes Kepler University Patterns Test Database (JKUPTD-Aug2013), is based on motifs and themes in Barlow and Morgenstern (1953), Schoenberg (1967), and Bruhn (1993). Repeated sections are based on those marked by the composer. These annotations are supplemented with some of our own where necessary. A Development Database (JKUPDD-Aug2013) enabled participants to try out their algorithms. For each piece in the Development and Test Databases, symbolic and synthesised audio versions are crossed with monophonic and polyphonic versions, giving four versions of the task in total: symPoly, symMono, audPoly, and audMono. There were no submissions to the audPoly or audMono categories this year, so two versions of the task ran. Submitted algorithms are shown in Table 1.
| Sub code | Submission name | Abstract | Contributors |
|---|---|---|---|
| Task Version | symPoly | ||
| CS7 | FindThemeAndSection_Poly | [ Tsung-Ping Chen] | |
| Task Version | symMono | ||
| CS3 | FindThemeAndSection_Mono | [ Tsung-Ping Chen] | |
| VM1'14 | VM1 | Gissel Velarde, David Meredith |
Table 1. Algorithms submitted to DRTS.
To compare these algorithms to the results or previous years, results of the representative versions of algorithms submitted in the previous years are presented as well. The following table shows which algorithms are compared against the new submissions.
| Sub code | Submission name | Abstract | Contributors | ||||
|---|---|---|---|---|---|---|---|
| Task Version | symPoly | ||||||
| DM1 | SIATECCompress-TLF1 | David Meredith | |||||
| DM2 | SIATECCompress-TLP | David Meredith | |||||
| DM3 | SIATECCompress-TLR | David Meredith | |||||
| OL1'14 | PatMinr | Olivier Lartillot | PLM1 | SYMCHM | Matevž Pesek, Urša Medvešek, Aleš Leonardis, Matija Marolt
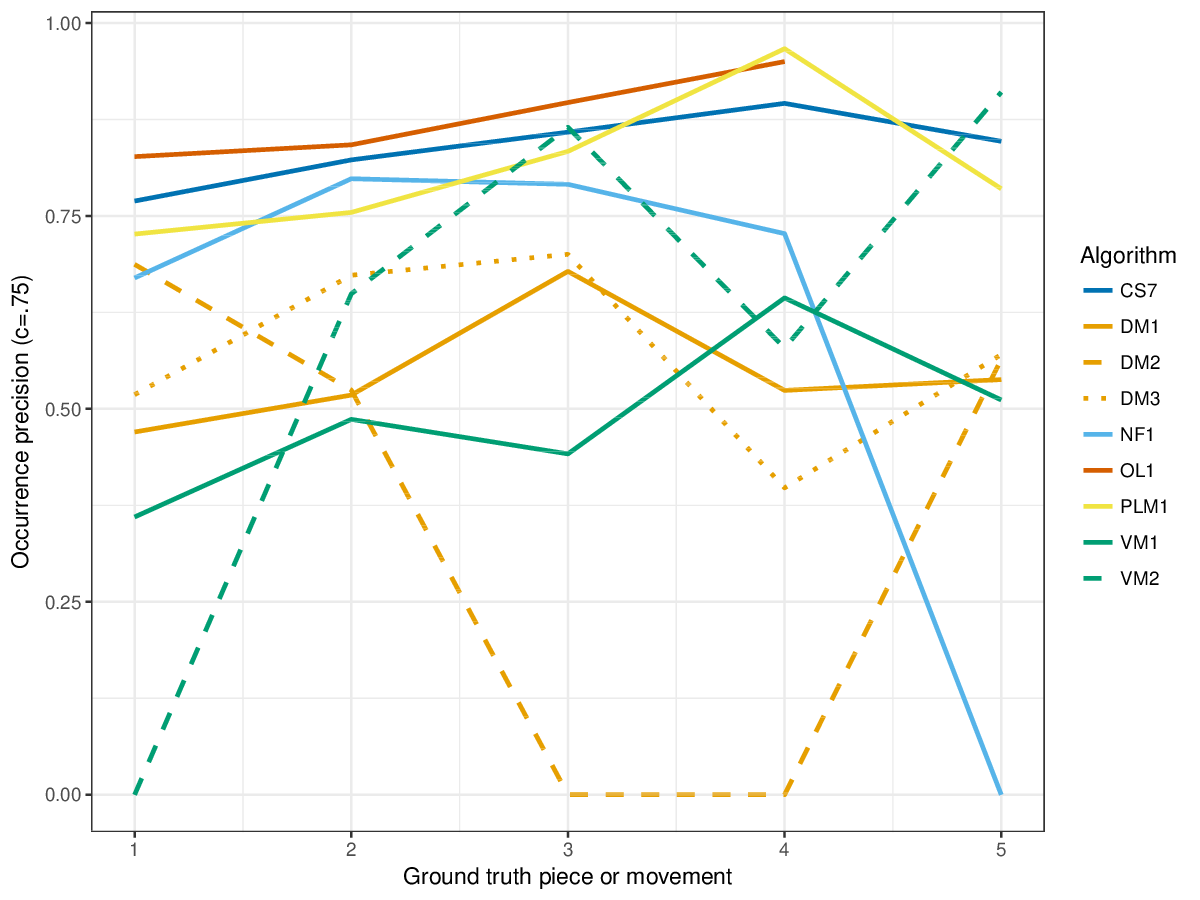
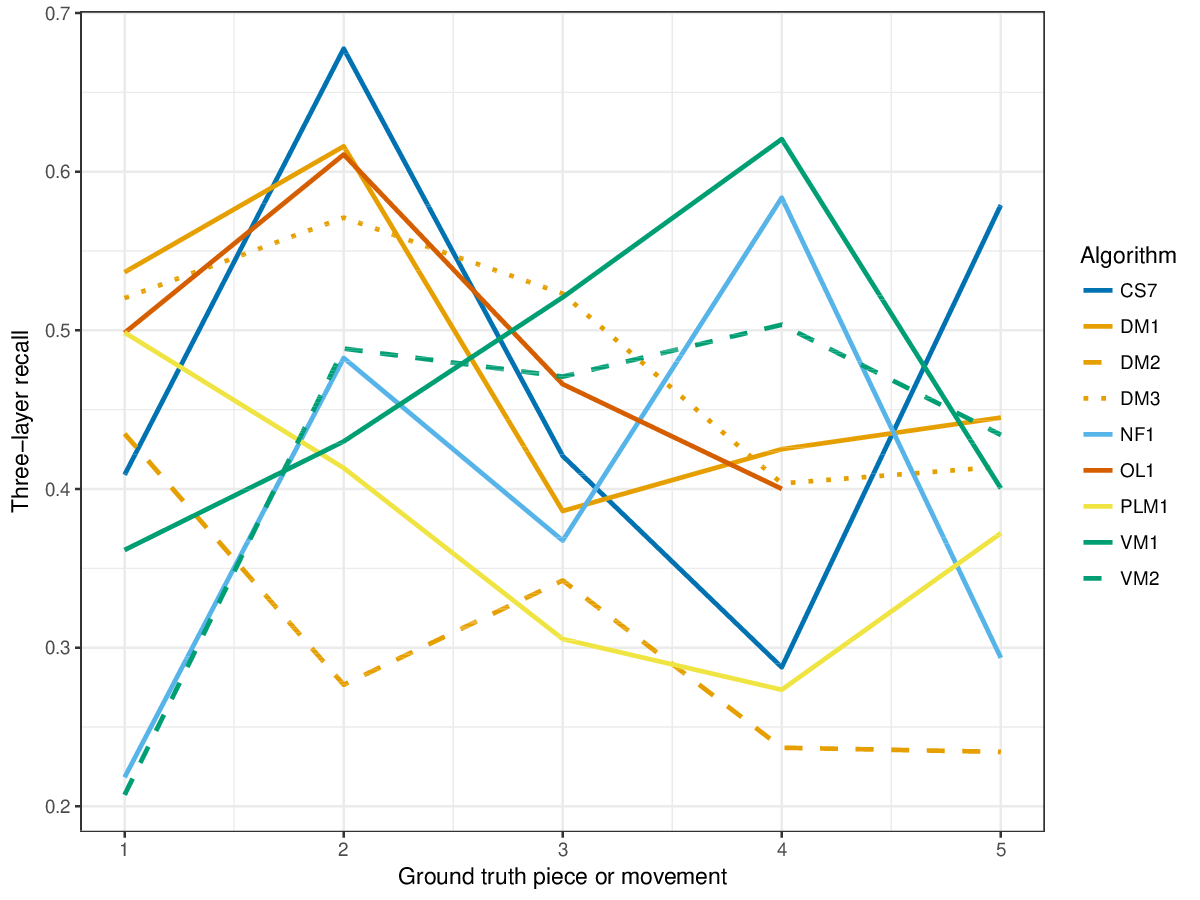
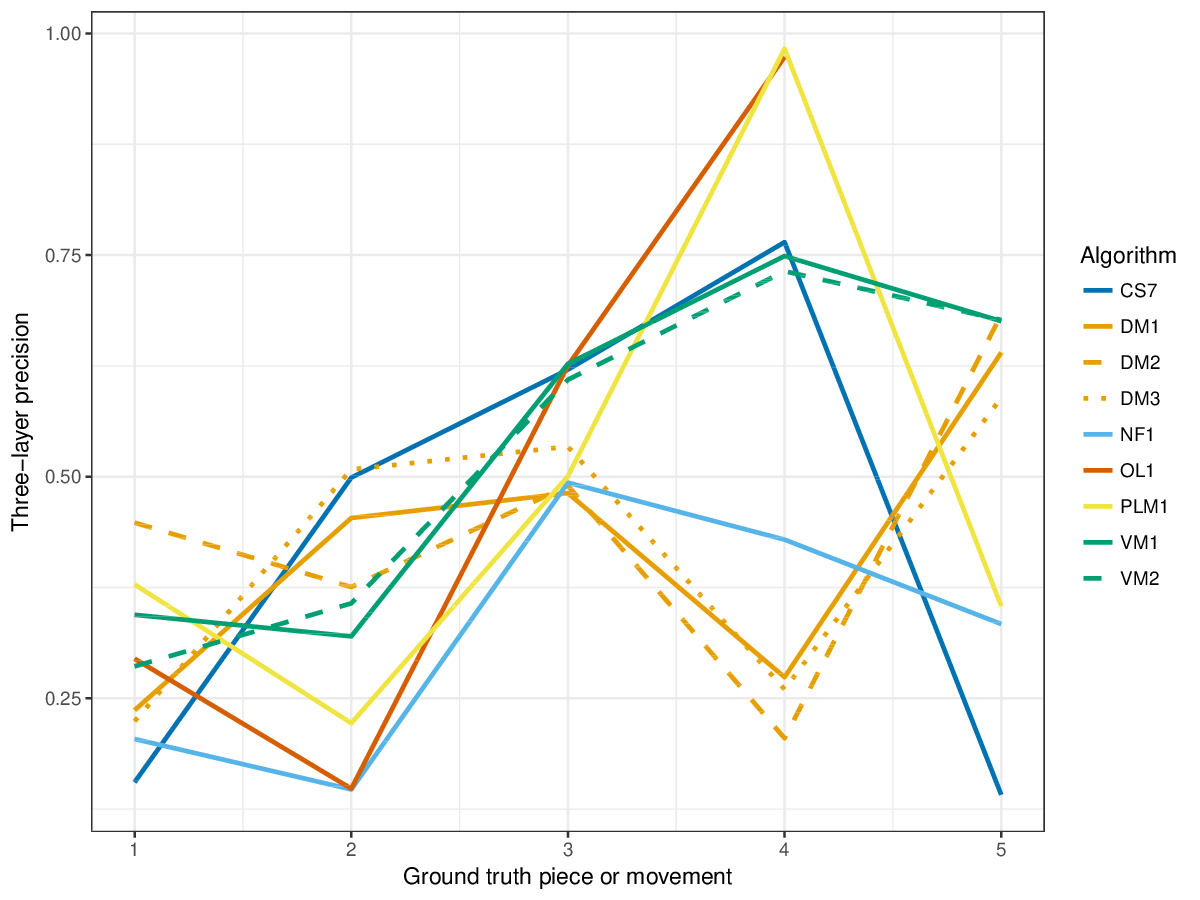
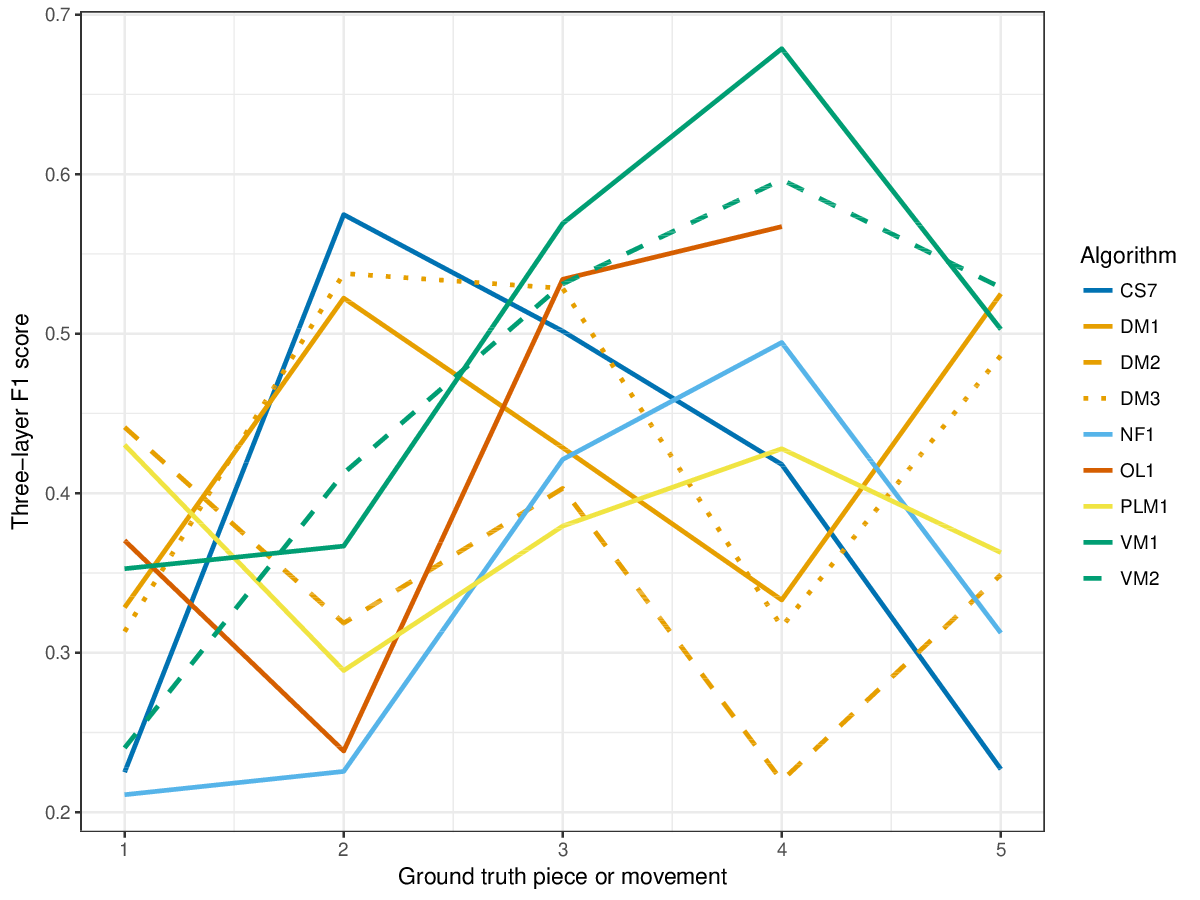
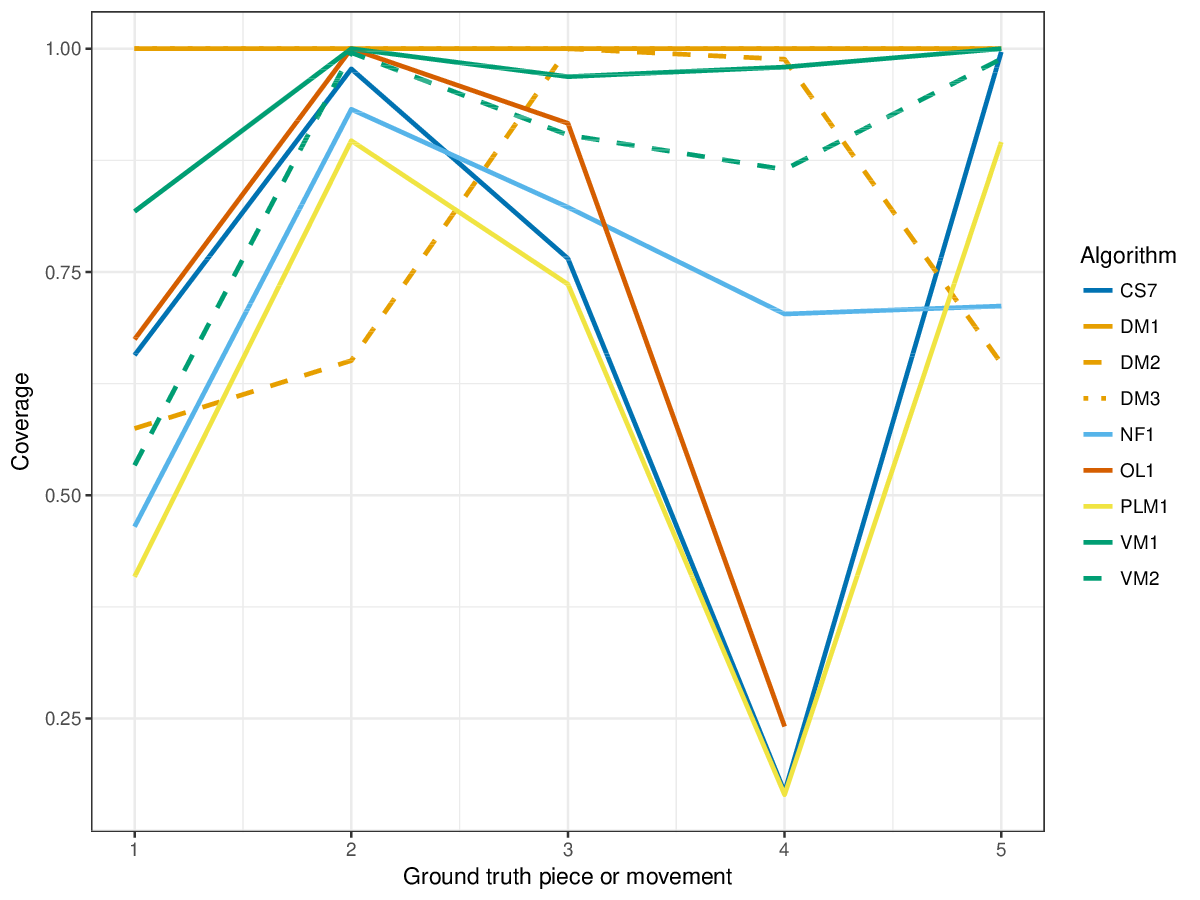
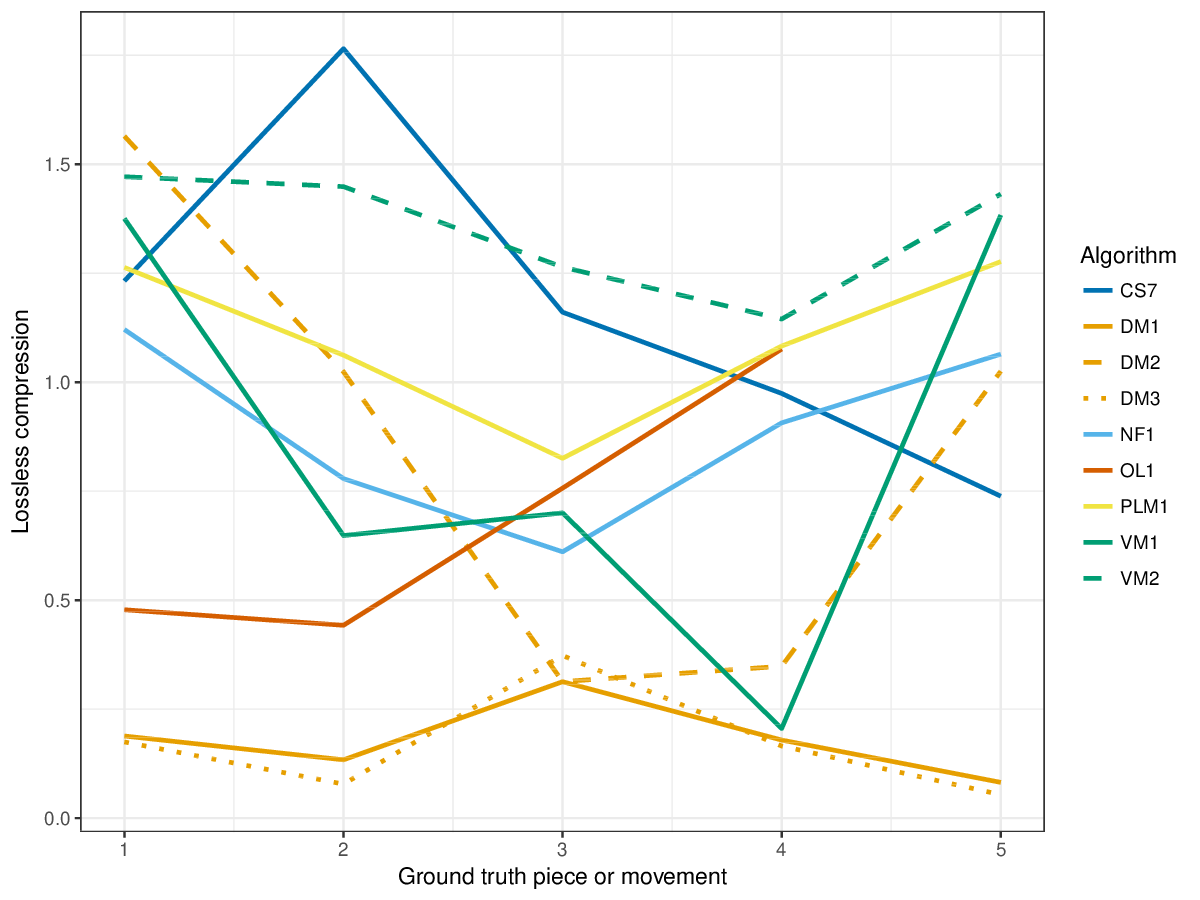
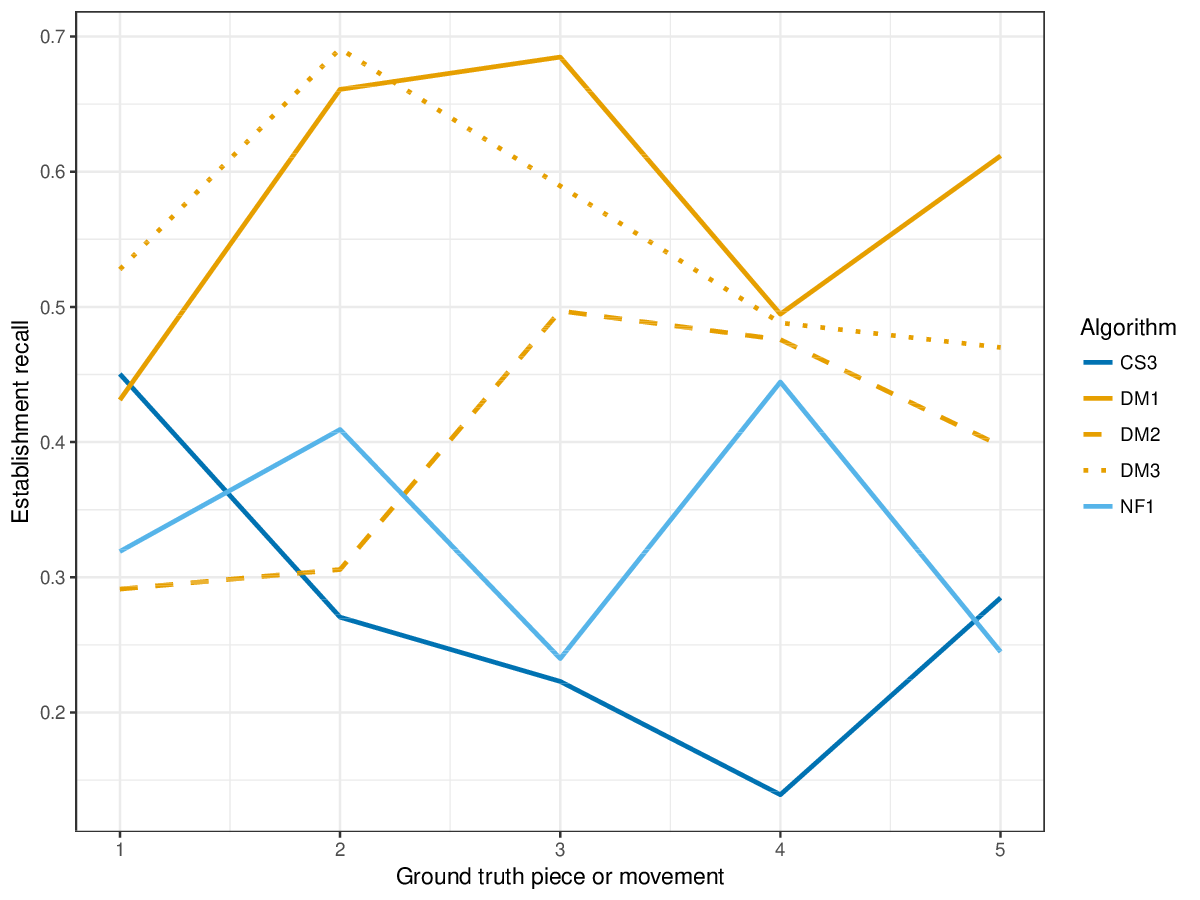
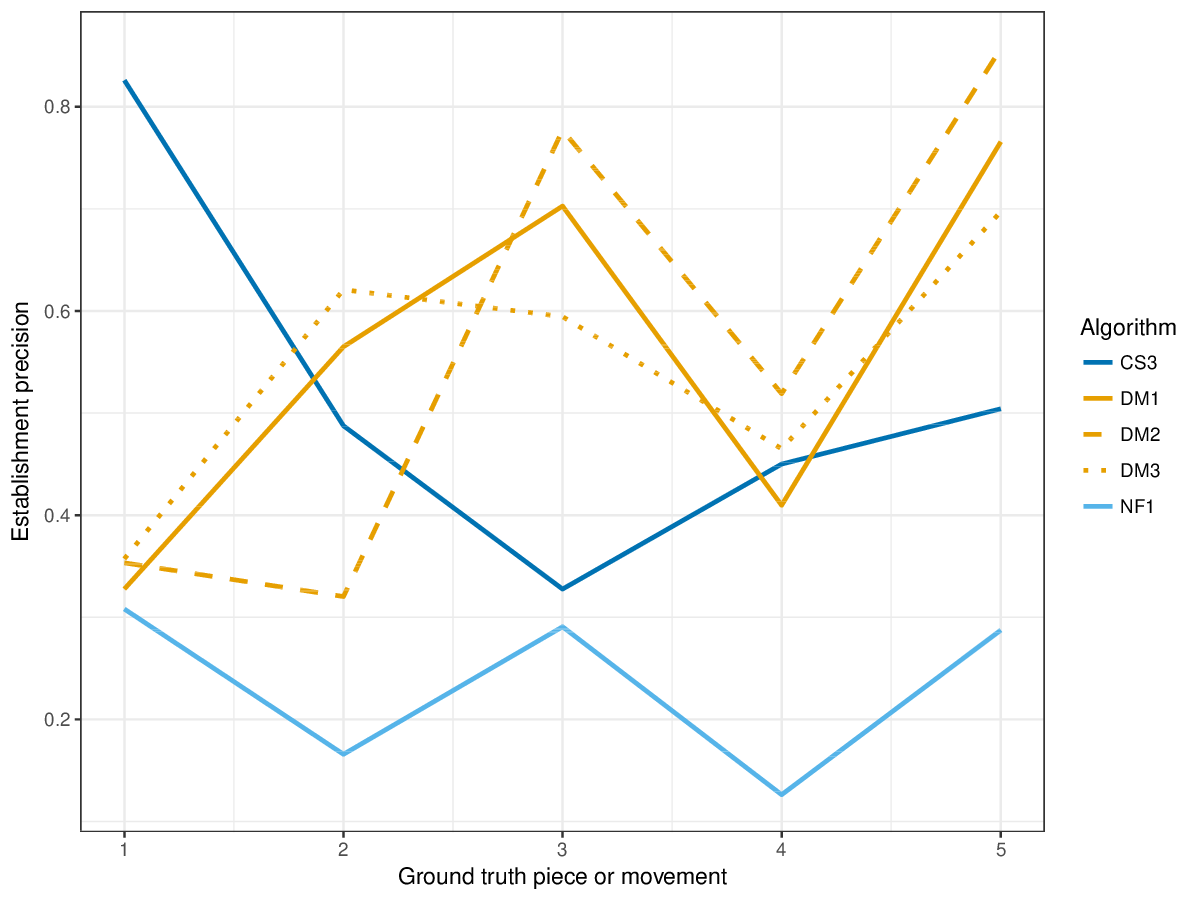
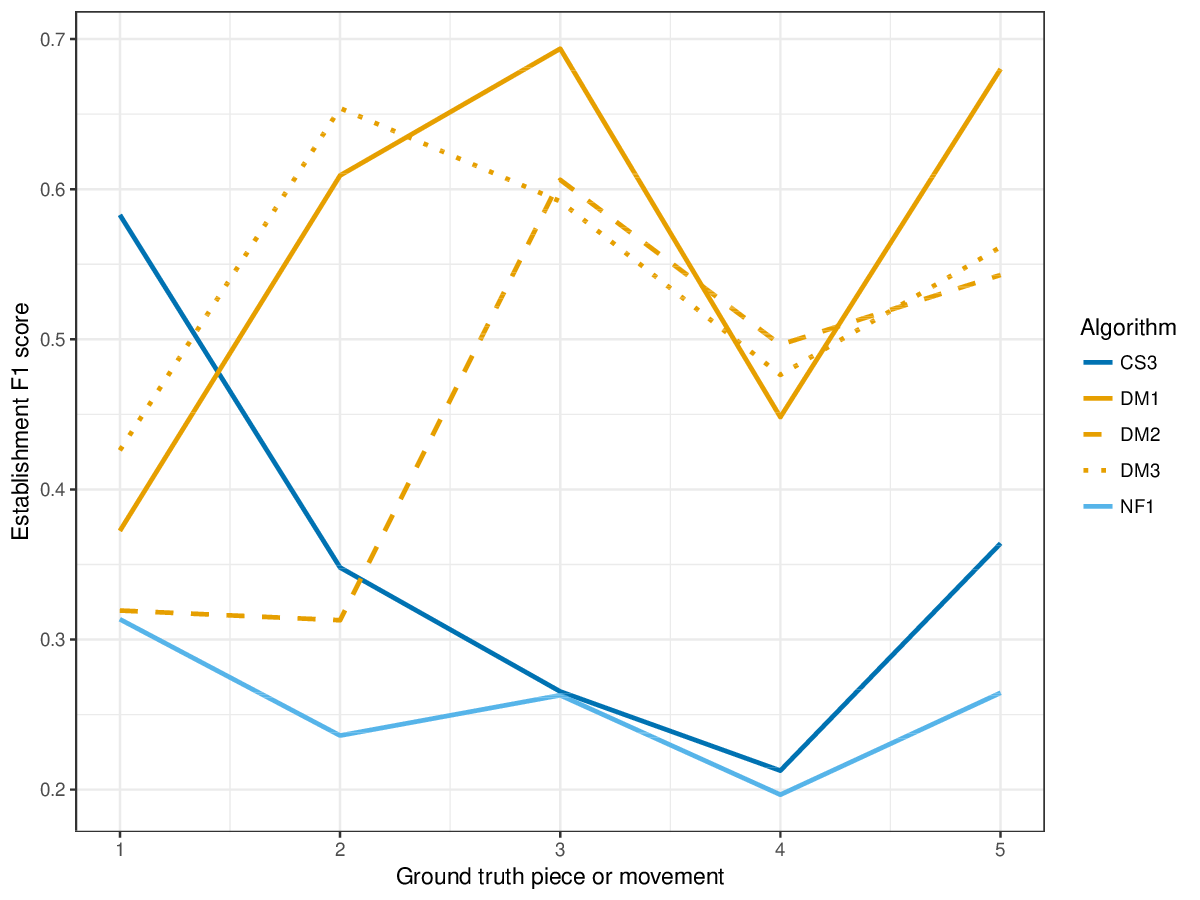
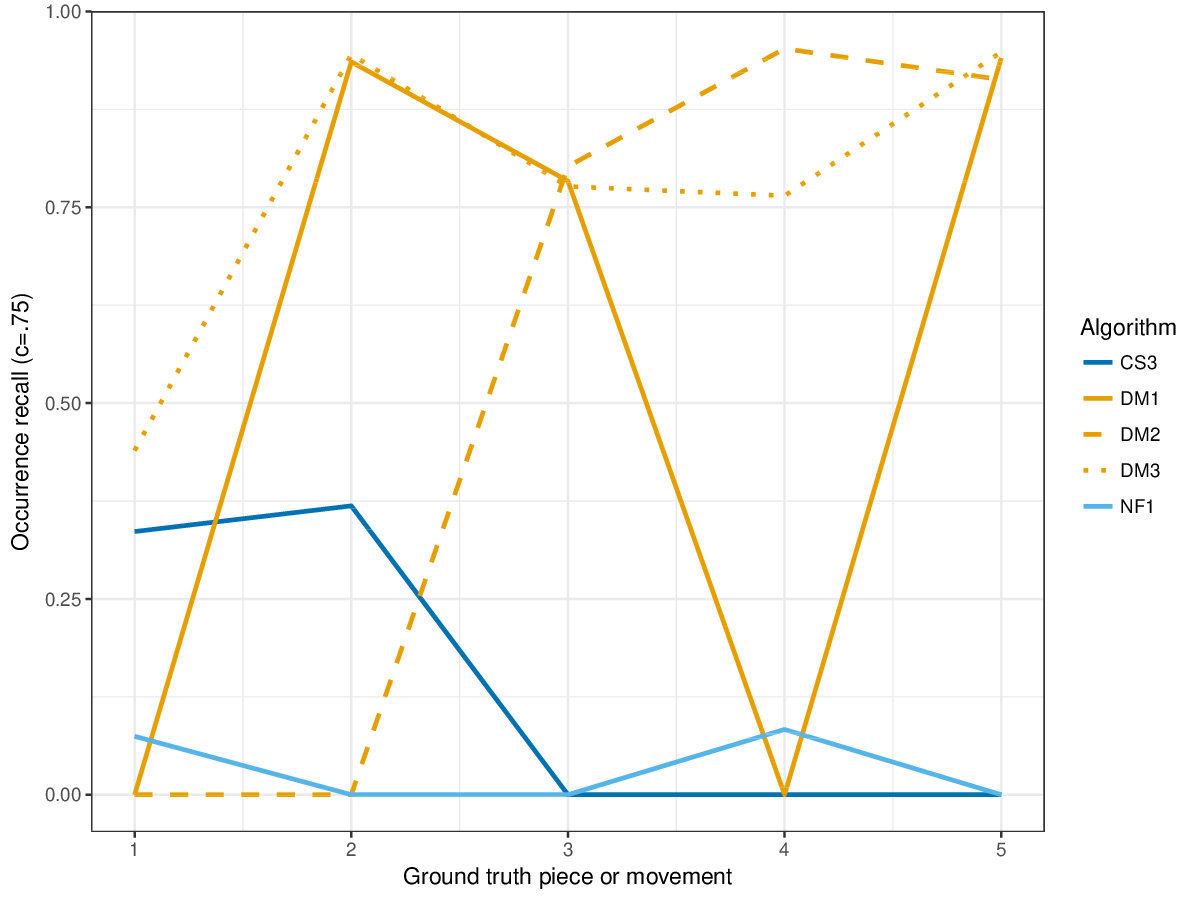
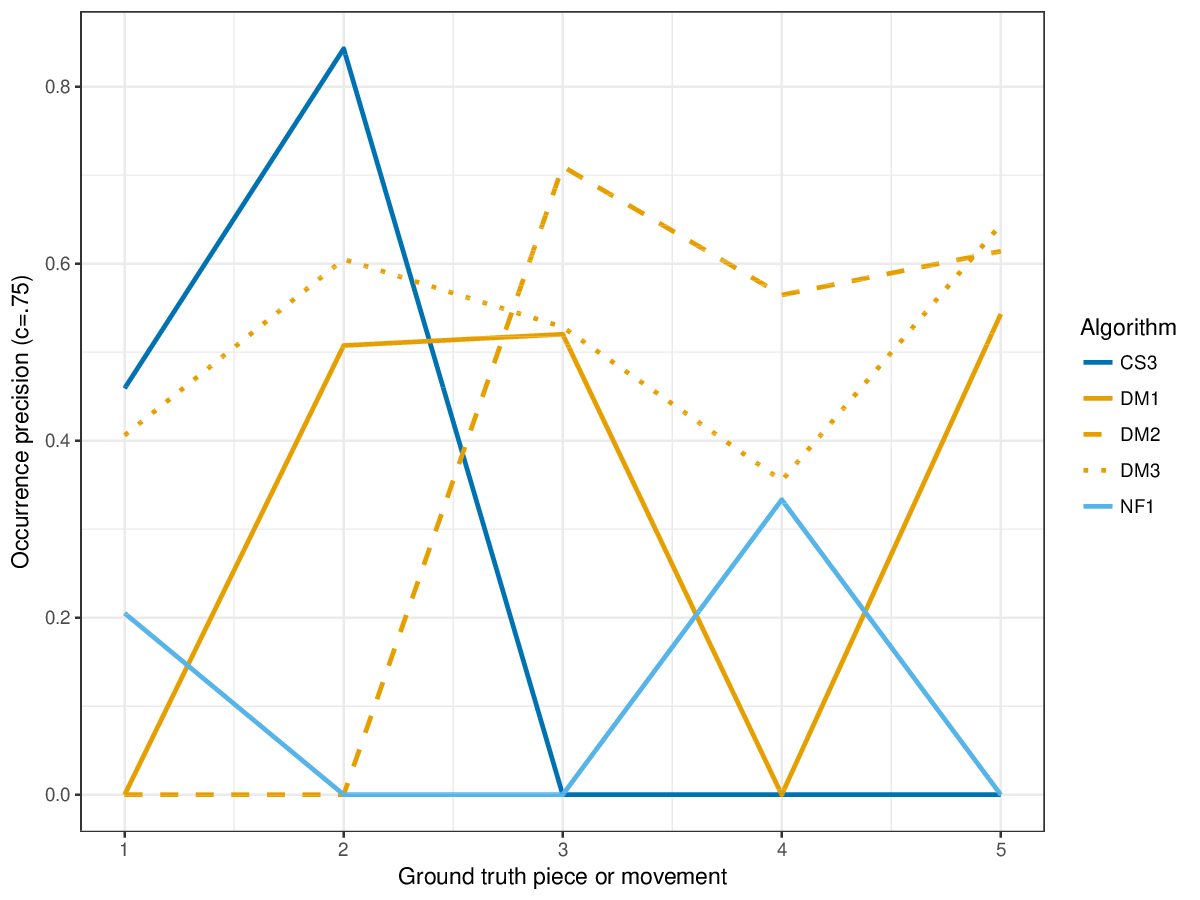
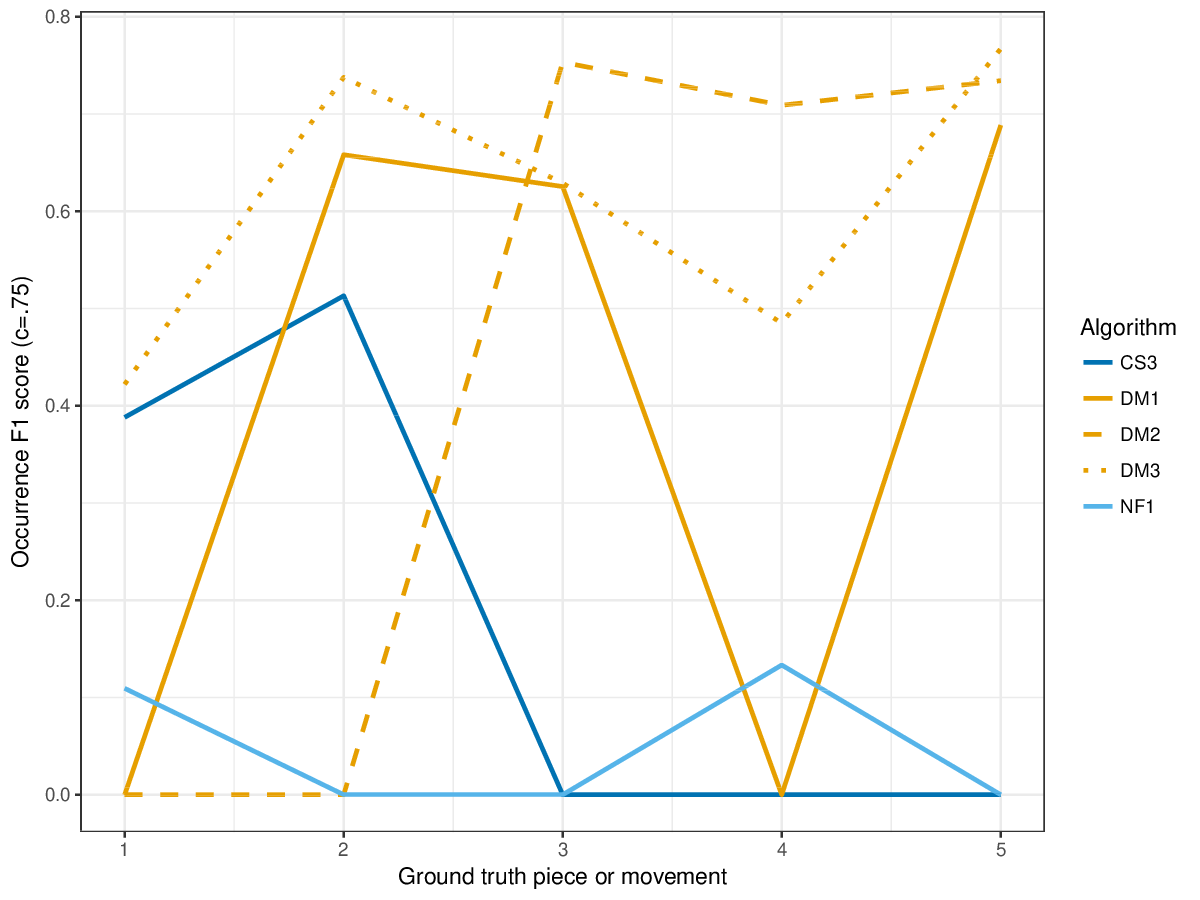
Results(For mathematical definitions of the various metrics, please see 2017:Discovery_of_Repeated_Themes_&_Sections#Evaluation_Procedure.) SymMonoSymPolyFigureslSymMonoSymPolyTablesSymMonoSymPoly |