2021:Patterns for Prediction

Description

In brief, there are two subtasks:

• Subtask 1) The Explicit Task - Algorithms that take an excerpt of music as input (the prime), and output a predicted continuation of the excerpt
• Subtask 2) The Implicit Task - Algorithms that are given a prime and a candidate continuation and return the probability that this is the true continuation of the provided prime (i.e. the notes which occur immediately after)

Your task captains are: Berit Janssen (berit.janssen), Iris YuPing Ren (yuping.ren.iris), James Owers (james.f.owers), and Tom Collins (tomthecollins, all at gmail.com). Please copy in all four of us if you have questions/comments. For participants interested in the 2021 edition, please also copy in Zongyu Yin (zy728 at york.ac.uk) instead of James Owers.

The submission deadline is Monday September 9th, 2019 (any time as long as it's Sep 9th somewhere on Earth!).

Relation to the pattern discovery task: The Patterns for Prediction task is an offshoot of the Discovery of Repeated Themes & Sections task (2013-2017). We hope to run the former (Patterns for Prediction) task and pause the latter (Discovery of Repeated Themes & Sections). In future years we may run both.

In more detail: One facet of human nature comprises the tendency to form predictions about what will happen in the future (Huron, 2006). Music, consisting of complex temporally extended sequences, provides an excellent setting for the study of prediction, and this topic has received attention from fields including but not limited to psychology (Collins, Tillmann, et al., 2014; Janssen, Burgoyne and Honing, 2017; Schellenberg, 1997; Schmukler, 1989), neuroscience (Koelsch et al., 2005), music theory (Gjerdingen, 2007; Lerdahl & Jackendoff, 1983; Rohrmeier & Pearce, 2018), music informatics (Conklin & Witten, 1995; Cherla et al., 2013), and machine learning (Elmsley, Weyde, & Armstrong, 2017; Hadjeres, Pachet, & Nielsen, 2016; Gjerdingen, 1989; Roberts et al., 2018; Sturm et al., 2016). In particular, we are interested in the way exact and inexact repetition occurs over the short, medium, and long term in pieces of music (Margulis, 2014; Widmer, 2016), and how these repetitions may interact with "schematic, veridical, dynamic, and conscious" expectations (Huron, 2006) in order to form a basis for successful prediction.

We call for algorithms that may model such expectations so as to predict the next musical events based on given, foregoing events (the prime). We invite contributions from all fields mentioned above (not just pattern discovery researchers), as different approaches may be complementary in terms of predicting correct continuations of a musical excerpt. We would like to explore these various approaches to music prediction in a MIREX task. For subtask (1) above (see "In brief"), the development and test datasets will contain an excerpt of a piece up until a cut-off point, after which the algorithm is supposed to generate the next N musical events up until 10 quarter-note beats, and we will quantitatively evaluate the extent to which an algorithm's continuation corresponds to the genuine continuation of the piece. For subtask (2), in addition to containing a prime, the development and test datasets will also contain continuations of the prime, one of which will be genuine, and the algorithm should rate the likelihood that each continuation is the genuine extension of the prime, which again will be evaluated quantitatively.

What is the relationship between pattern discovery and prediction? The last five years have seen an increasing interest in algorithms that discover or generate patterned data, leveraging methods beyond typical (e.g., Markovian) limits (Collins & Laney, 2017; MIREX Discovery of Repeated Themes & Sections task; Janssen, van Kranenburg and Volk, 2017; Ren et al., 2017; Widmer, 2016). One of the observations to emerge from the above-mentioned MIREX pattern discovery task is that an algorithm that is "good" at discovering patterns ought to be extendable to make "good" predictions for what will happen next in a given music excerpt (Meredith, 2013). Furthermore, evaluating the ability to predict may provide a stronger (or at least complementary) evaluation of an algorithm's pattern discovery capabilities, compared to evaluating its output against expert-annotated patterns, where the notion of "ground truth" has been debated (Meredith, 2013).

Data

The Patterns for Prediction Development Dataset (PPDD-Sep2018) has been prepared by processing a randomly selected subset of the Lakh MIDI Dataset (LMD, Raffel, 2016). It has audio and symbolic versions crossed with monophonic and polyphonic versions. The audio is generated from the symbolic representation, so it is not "expressive". The symbolic data is presented in CSV format. For example,

20,64,62,0.5,0
20.66667,65,63,0.25,0
21,67,64,0.5,0
...

would be the start of a prime where the first event had ontime 20 (measured in quarter-note beats -- equivalent to bar 6 beat 1 if the time signature were 4-4), MIDI note number (MNN) 64, estimated morphetic pitch number 62 (see p. 352 from Collins, 2011 for a diagrammatic explanation; for more details, see Meredith, 1999), duration 0.5 in quarter-note beats, and channel 0. Re-exports to MIDI are also provided, mainly for listening purposes. We also provide a descriptor file containing the original Lakh MIDI Dataset id, the BPM, time signature, and a key estimate. The audio dataset contains all these files, plus WAV files. Therefore, the audio and symbolic variants are identical to one another, apart from the presence of WAV files. All other variants are non-identical, although there may be some overlap, as they were all chosen from LMD originally.

The provenance of the Patterns for Prediction Test Dataset (PPTD) will not be disclosed, but it is not from LMD, if you are concerned about overfitting.

There are small (100 pieces), medium (1,000 pieces), and large (10,000 pieces) variants of each dataset, to cater to different approaches to the task (e.g., a point-set pattern discovery algorithm developer may not want/need as many training examples as a neural network researcher). Each prime lasts approximately 35 sec (according to the BPM value in the original MIDI file) and each continuation covers the subsequent 10 quarter-note beats. We would have liked to provide longer primes (as 35 sec affords investigation of medium- but not really long-term structure), but we have to strike a compromise between ideal and tractable scenarios.

Here are the PPDD-Sep2018 variants for download:

• audio, monophonic, small (92 MB)
• audio, monophonic, medium (850 MB)
• audio, monophonic, large (8.46 GB)
• audio, polyphonic, small (137 MB)
• audio, polyphonic, medium (1.35 GB)
• audio, polyphonic, large (13.44 GB)
• symbolic, monophonic, small (< 1 MB)
• symbolic, monophonic, medium (3 MB)
• symbolic, monophonic, large (32 MB)
• symbolic, polyphonic, small (< 1 MB)
• symbolic, polyphonic, medium (9 MB)
• symbolic, polyphonic, large (64 MB)

("Large" datasets were compressed using the p7zip package, installed via "brew install p7zip on Mac".)

Some examples

This prime finishes with two G’s followed by a D above. Looking at the piano roll or listening to the linked file, we can see/hear that this pitch pattern, in the exact same rhythm, has happened before (see bars 17-18 transition in the piano roll). Therefore, we and/or an algorithm, might predict that the first note of the continuation will follow the pattern established in the previous occurrence, returning to G 1.5 beats later.

This is another example where a previous occurrence of a pattern might help predict the contents of the continuation. Not all excerpts contain patterns (in fact, one of the motivations for running the task is to interrogate the idea that patterns are abundant in music and always informative in terms of predicting what comes next). This one, for instance, does not seem to contain many clues for what will come next. And finally, this one might not contain any obvious patterns, but other strategies (such as schematic or tonal expectations) might be recruited in order to predict the contents of the continuation.

(These examples are from an earlier version of the dataset, PPDD-Jul2018, but the above observations apply also to the current version of the dataset.)

Preparation of the data

Preparation of the monophonic datasets was more involved than the polyphonic datasets: for both, we imported each MIDI file, quantised it using a subset of the Farey sequence of order 6 (Collins, Krebs, et al., 2014), and then excerpted a prime and continuation at a randomly selected time. For the monophonic datasets, we filtered for:

• channels that contained at least 20 events in the prime;
• channels that were at least 80% monophonic at the outset, meaning that at least 80% of their segments (Pardo & Birmingham, 2002) contained no more than one event;
• channels where the maximum inter-ontime interval in the prime was no more than 8 quarter-note beats.
• we then "skylined" these channels (independently) so that no two events had the same start time (maximum MNN chosen in event of a clash), and double-checked that they still contained at least 20 events;
• one suitable channel was then selected at random, and the prime appears in the dataset if the continuation contained at least 10 events.

If any of the above could not be satisfied for the given input, we skipped this MIDI file.

For the polyphonic data, we applied the minimum note criteria of 20 in the prime and 10 in the continuation, as well as the prime maximum inter-ontime interval of 8, but it was not necessary to measure monophony or perform skylining.

Audio files were generated by importing the corresponding CSV and descriptor files and using a sample bank of piano notes from the Google Magenta NSynth dataset (Engel et al., 2017) to construct and export the waveform.

The foil continuations were generated using a Markov model of order 1 over the whole texture (polyphonic) or channel (monophonic) in question, and there was no attempt to nest this generation process in any other process cognisant of repetitive or phrasal structure. See Collins and Laney (2017) for details of the state space and transition matrix.

Submission Format

In terms of input representations, we will evaluate 4 largely independent versions of the task: audio, monophonic; audio, polyphonic; symbolic, monophonic; symbolic, polyphonic. Participants may submit algorithms to 1 or more of these versions, and should list these versions clearly in their readme. Irrespective of input representation, all output for subtask (1) should be in "ontime", "MNN" CSV files. The CSV may contain other information, but "ontime" and "MNN" should be in the first two columns, respectively. All output for subtask (2) should be an indication whether of the two presented continuations, "A" or "B" is judged by the algorithm to be genuine. This should be one CSV file for an entire dataset, with first column "id" referring to the file name of a prime-continuation pair, second column "A" containing a likelihood value in [0, 1] for the genuineness of the continuation in folder A, and column "B" similarly for the continuation in folder B.

All submissions should be statically linked to all dependencies and include a README file including the following information:

• input representation(s), should be 1 or more of "audio, monophonic"; "audio, polyphonic"; "symbolic, monophonic"; "symbolic, polyphonic";
• subtasks you would like your algorithm to be evaluated on, should be "1", "2", or "1 and 2" (see first sentences of 2018:Patterns_for_Prediction#Description for a reminder);
• command line calling format for all executables and an example formatted set of commands;
• number of threads/cores used or whether this should be specified on the command line;
• expected memory footprint;
• expected runtime;
• any required environments and versions, e.g. Python, Java, Bash, MATLAB.

Example Command Line Calling Format

Python:

python <your_script_name.py> -i <input_folder> -o <output_folder>

Evaluation Procedure

In brief:

• For subtask 1), we match the algorithmic output with the original continuation and compute a match score which is described below. We additionally provide a pitch score which ignores rhythm.
• For subtask 2), we return the accuracy: the count of how many times an algorithm judged the genuine continuation as most likely. Additionally we return the mean and variance of the predicted probability for the true continuation (the higher the mean and lower the variance the better)

The code used for all evaluations is available on GitHub.

Notation

The input excerpt ends with a final note event: $(x_{0},y_{0})$, where $x_{0}$ is ontime (start time measured in quarter-note beats starting with 0 for bar 1 beat 1), $y_{0}$ is pitch, represented by MNN.

For subtask 1, the algorithm predicts the continuations: $({\hat {x}}_{1},{\hat {y}}_{1})$, $({\hat {x}}_{2},{\hat {y}}_{2})$, ..., $({\hat {x}}_{n^{\prime }},{\hat {y}}_{n^{\prime }})$, where ${\hat {x}}_{i}$ are predicted ontimes, and ${\hat {y}}_{i}$ are predicted MNNs. The true continuations are notated $(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})$. The predicted continuation ontimes are strictly non-decreasing, that is ${\hat {x}}_{0}\leq {\hat {x}}_{1}\leq \cdots \leq {\hat {x}}_{n^{\prime }}$, and so are the true continuation ontimes, that is $x_{0}\leq x_{1}\leq \cdots \leq x_{n}$.

Subtask 1 - Explicit Task

For subtask 1, the algorithm is provided with a prime, and produces a continuation. We clip this continuation at 10 beats long (plus the time for the last note to finish). We then compare the generated continuation with the true continuation using two different scores: the cardinality and pitch score. In short, the cardinality score attempts to find the best overlap be between the continuations, and the pitch score makes a histogram of pitches for both continuations and checks the overlap between them.

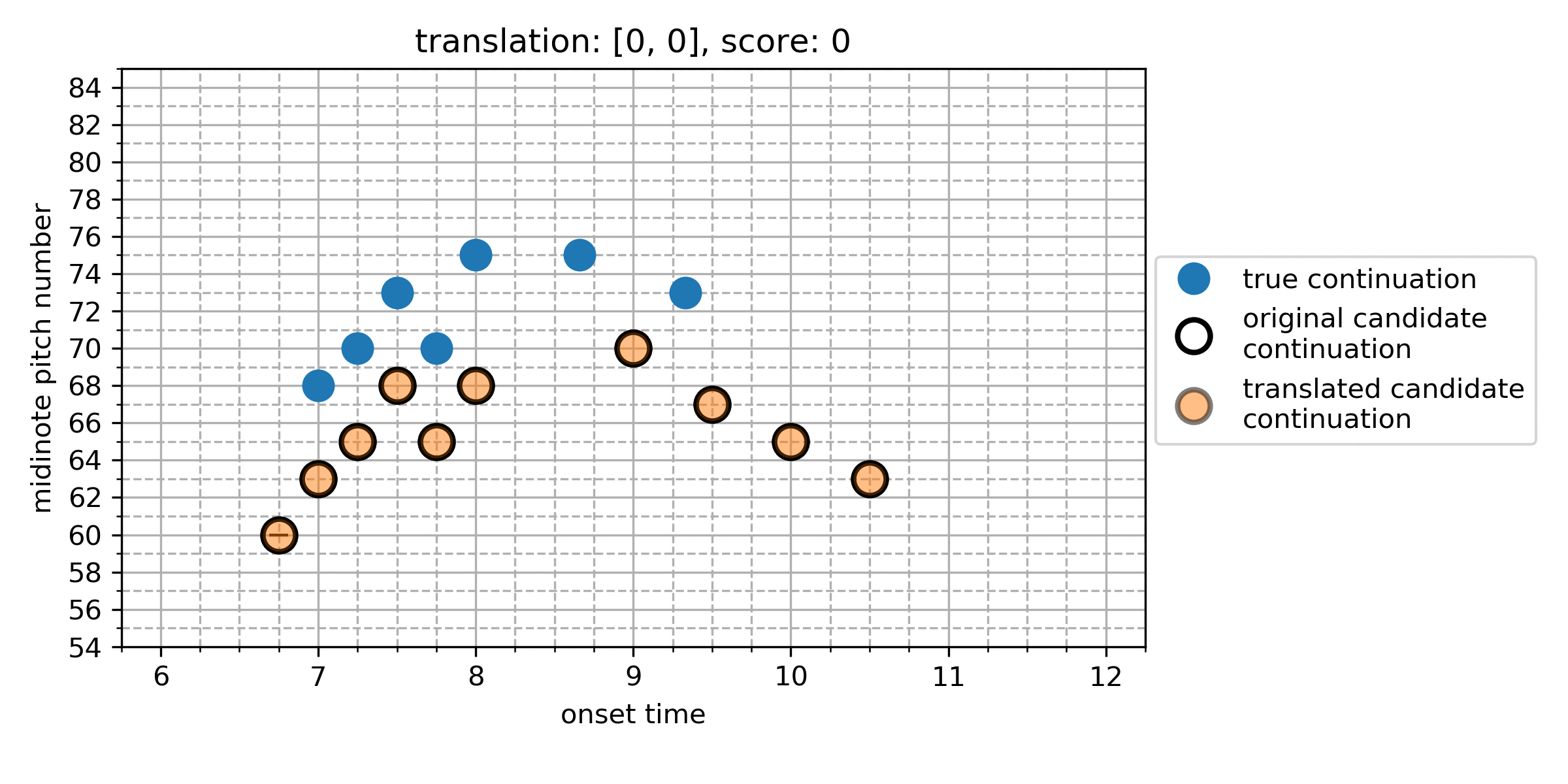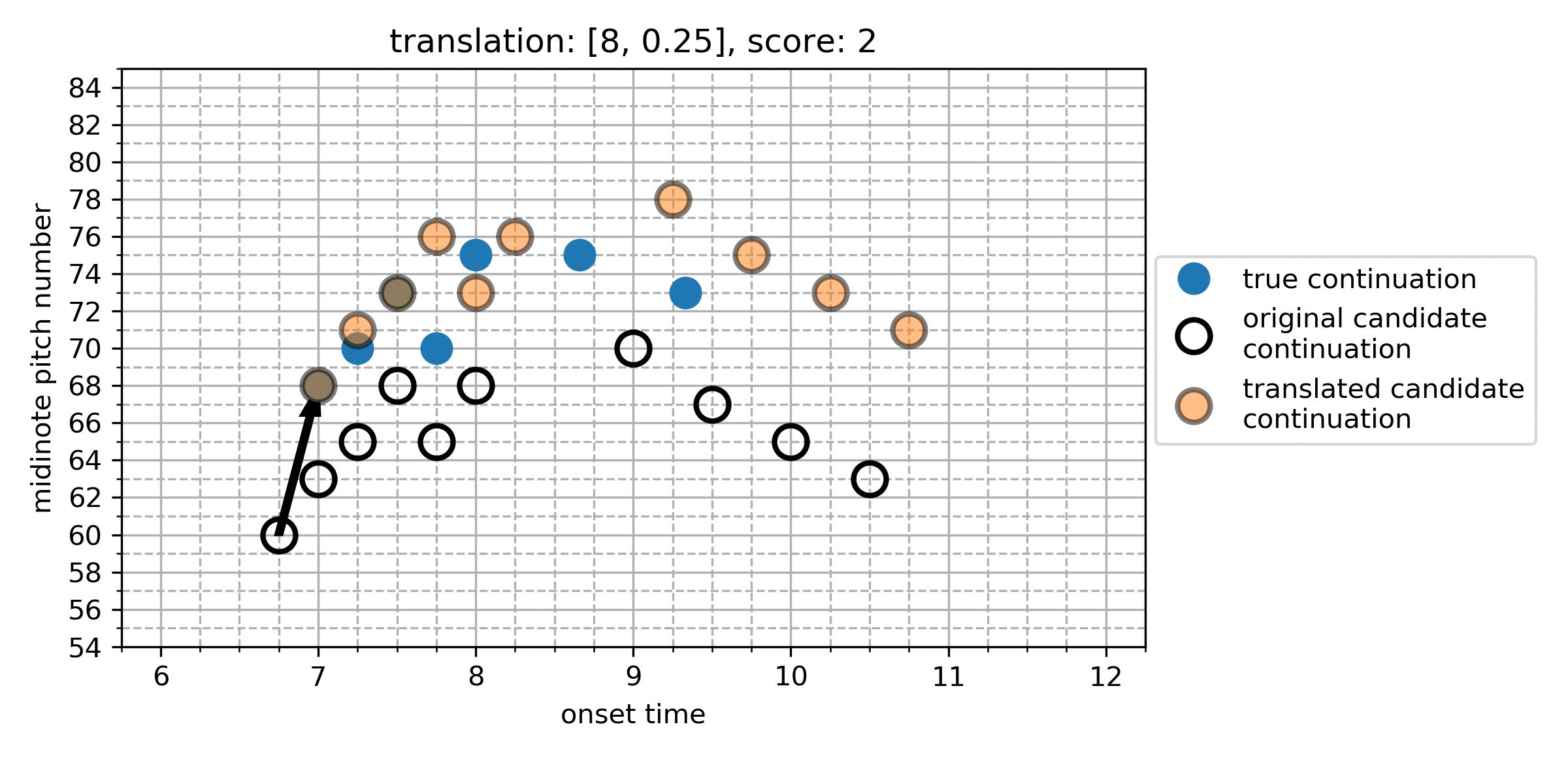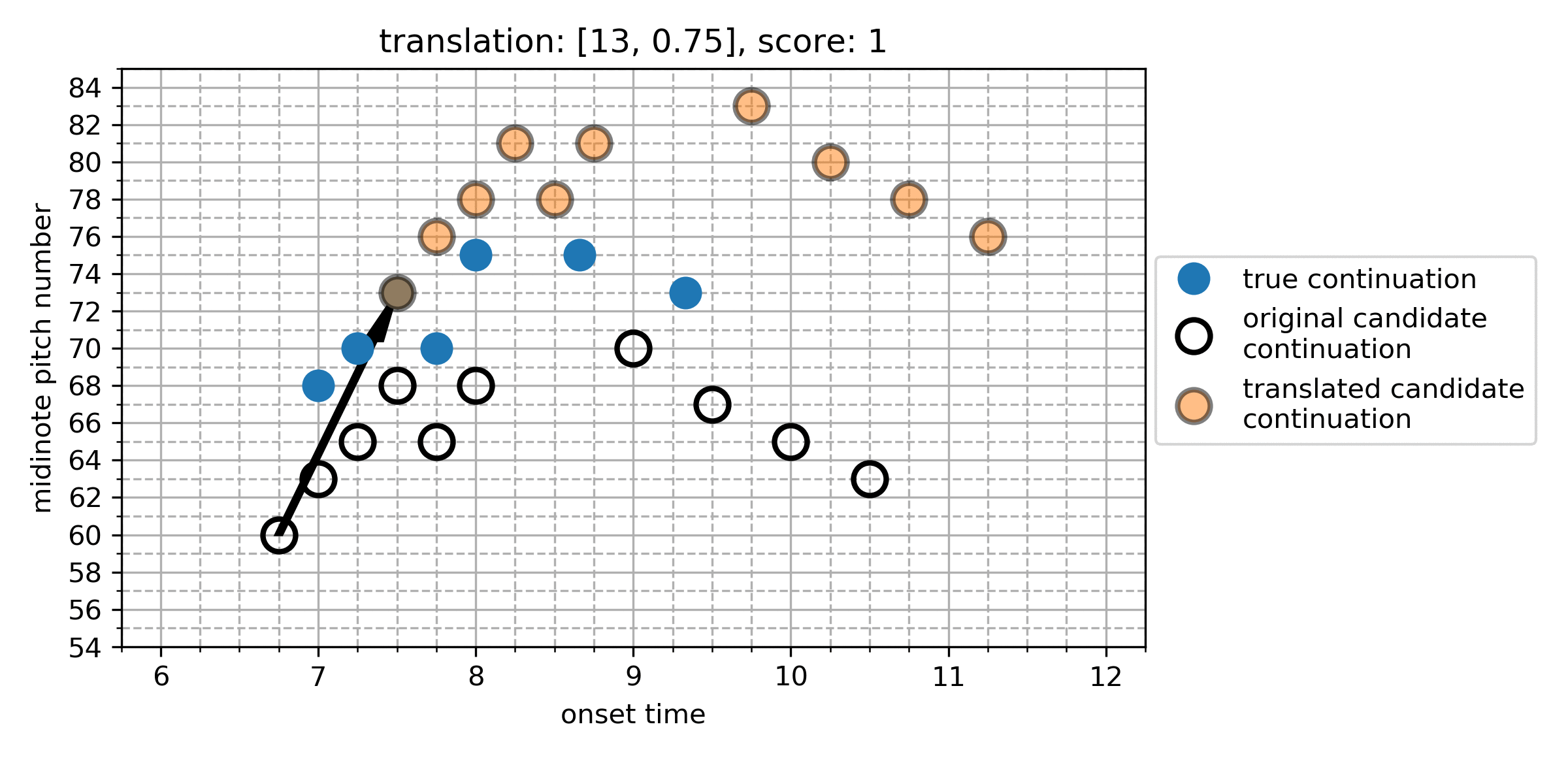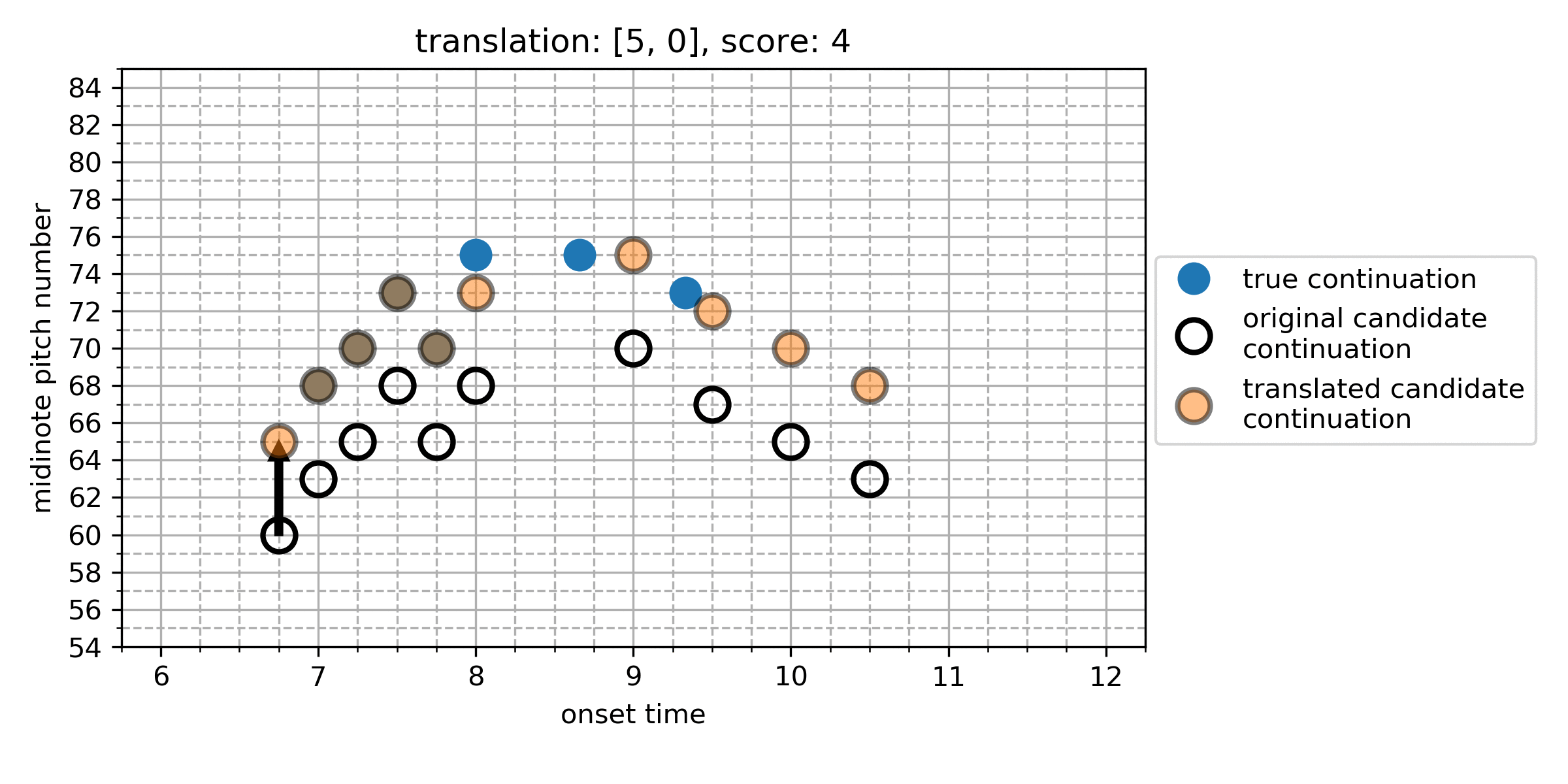
The Cardinality Score

We represent each note in the true and algorithmic continuation as a point in a two-dimensional space of onset and pitch, giving the point-set $\mathbf {P} =\{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{n},y_{n})\}$ for the true continuation, and $\mathbf {Q} =\{({\hat {x}}_{1},{\hat {y}}_{1}),({\hat {x}}_{2},{\hat {y}}_{2}),...,({\hat {x}}_{n^{\prime }},{\hat {y}}_{n^{\prime }})\}$ for the algorithmic continuation. We calculate differences between all points $p=(x_{i},y_{i})$ in $\mathbf {P}$ and $q=({\hat {x}}_{j},{\hat {y}}_{j})$ in $\mathbf {Q}$, which represent the translation vectors $\mathbf {T}$ that transform a given algorithmically generated note into a note from the true continuation:

$\mathbf {T} =\left\{p-q\;\forall \;p\in \mathbf {P} ,\,q\in \mathbf {Q} \right\}$

From this, we find the $t\in \mathbf {T}$ which maximises the cardinality of the set of notes which now overlap under this translation. The maximum cardinality is the Cardinality Score (CS):

${\text{CS}}(\mathbf {P} ,\mathbf {Q} )=\max _{t\in \mathbf {T} }\left|\left\{q\;\forall \;q\in \mathbf {Q} \;\,|\;\,(q+t)\in \mathbf {P} \right\}\right|$

Here is an illustration of the search for the CS:

Figure 1. An illustration of the search for the cardinality score. In this case, translating the candidate continuation up by 5 semitones (and no temporal shift) gives the CS of 4.

We define recall as the number of correctly predicted notes, divided by the cardinality of the true continuation point set $\mathbf {P}$. Since there exists at least one point in $\mathbf {Q}$ which can be translated by any vector to a point in $\mathbf {P}$, we subtract $1$ from numerator and denominator to scale to $[0,1]$.

${\text{Rec}}=({\text{cs}}(\mathbf {P} ,\mathbf {Q} )-1)/(|\mathbf {P} |-1)$

Precision is the number of correctly predicted notes, divided by the cardinality of the point set of the algorithmic continuation $\mathbf {Q}$, scaled in the same way:

${\text{Prec}}=({\text{cs}}(\mathbf {P} ,\mathbf {Q} )-1)/(|\mathbf {Q} |-1)$

The Pitch Score

The cardinality rewards continuations that are the correct 'shape' - it will give the maximum score to a continuation which is a copy of the true continuation but transposed one semitone down. This is not a very musically correct continuation! To counter this in some way, we also asses the pitches of the continuations more directly.

To do this we create two normalised histograms of the pitches in both continuations. The score is simply the overlap between the overlaid histograms (maximum score is 1, minimum is 0).

We then repeat the process but disregard octave (i.e. take the MNN pitch modulo 12).

A note on Entropy

Some existing work in this area (e.g., Conklin & Witten, 1995; Pearce & Wiggins, 2006; Temperley, 2007) evaluates algorithm performance in terms of entropy. If we have time to collect human listeners' judgments of likely (or not) continuations for given excerpts, then we will be in a position to compare the entropy of listener-generated distributions with the corresponding algorithm distributions. This would open up the possibility of entropy-based metrics, but we consider this of secondary importance to the metrics outlined above.

Subtask 2 - Implicit Task

For subtask two, we provide each model with a prime and continuation and it returns the probability that this is the true continuation. We only provide two continuations - the true continuation, and a foil continuation generated by our baseline markov model. We then softmax these values such that the sum of probabilities for the two continuations is 1. The best model should assign a high probability to the true continuation (1) and a low continuation to the foil continuation (0).

Accuracy

To get the accuracy of the model, we simply sum the number of times it assigns a higher probability for the true continuation.

Average Probability

It's possible models could attain a similar accuracy but assign different probabilities e.g. one model gets an accuracy of 1 but gives the true continuations a probability of around .51, whereas another could predict near 1 for the true continuations. To identify more confident models, and get a slightly more in depth understanding of model performance, we also take the mean and variance of the probability assigned to the true continuation. The non-informative model (assigning .5 to all inputs), will get a mean probability score of .5, the minimum score is 0, and the maximum score is of course 1.

Questions (Q), Answers (A), and Comments (C)

Q. Instead of evaluating continuations, have you considered evaluating an algorithm's ability to predict content between two timepoints, or before a timepoint?

A. Yes we considered including this also, but opted not to for sake of simplicity. Furthermore, these alternatives do not have the same intuitive appeal as predicting future events.

Q. Why do some files sound like they contain a drum track rendered on piano?

A. Some of the MIDI files import as a single channel, but upon listening to them it is evident that they contain multiple instruments. For the sake of simplicity, we removed percussion channels where possible, but if everything was squashed down into a single channel, there was not much we could do.

C. to_the_sun--at--gmx.com writes: "This is exactly what I'm interested in! I have an open-source project called The Amanuensis (https://github.com/to-the-sun/amanuensis) that uses an algorithm to predict where in the future beats are likely to fall.

"Amanuensis constructs a cohesive song structure, using the best of what you give it, looping around you and growing in real-time as you play. All you have to do is jam and fully written songs will flow out behind you wherever you go.

"My algorithm right now is only rhythm-based and I'm sure it's not sophisticated enough to be entered into your contest, but I would be very interested in the possibility of using any of the algorithms that are, in place of mine in The Amanuensis. Would any of your participants be interested in some collaboration? What I can bring to the table would be a real-world application for these algorithms, already set for implementation."

Q. I'm interested in performing this task on the symbolic dataset, but I don't have an audio-based algorithm. It was unclear to me if the inputs are audio, symbolic, both, or either.

A. We have clarified, at the top of 2018:Patterns_for_Prediction#Submission_Format, that submissions in 1-4 representational categories are acceptable. It's also OK, say, for an audio-based algorithm to make use of the descriptor file in order to determine beat locations. (You could do this by looking at the $u=\mathrm {bpm}$ value, and then you would know that the main beats in the WAV file are at $0,60/u,2\cdot 60/u,\ldots$ sec.)

Time and Hardware Limits

A total runtime limit of 72 hours will be imposed on each submission.

Seeking Contributions

• We would like to evaluate against real (not just synthesized-from-MIDI) audio versions. If you have a good idea of how we might make this available to participants, let us know. We would be happy to acknowledge individuals and/or companies for helping out in this regard.

• More suggestions/comments/ideas on the task is always welcome!

Acknowledgments

Thank you to Anja Volk, Darrell Conklin, Srikanth Cherla, David Meredith, Matevz Pesek, and Gissel Velarde for discussions!

References

• Cherla, S., Weyde, T., Garcez, A., and Pearce, M. (2013). A distributed model for multiple-viewpoint melodic prediction. In In Proceedings of the International Society for Music Information Retrieval Conference (pp. 15-20). Curitiba, Brazil.

• Collins, T. (2011). "Improved methods for pattern discovery in music, with applications in automated stylistic composition". PhD Thesis.

• Collins, T., Böck, S., Krebs, F., & Widmer, G. (2014). Bridging the audio-symbolic gap: The discovery of repeated note content directly from polyphonic music audio. In Proceedings of the Audio Engineering Society's 53rd Conference on Semantic Audio. London, UK.

• Collins, T., Tillmann, B., Barrett, F. S., Delbé, C., & Janata, P. (2014). A combined model of sensory and cognitive representations underlying tonal expectations in music: From audio signals to behavior. Psychological Review, 121(1), 33-65.

• Collins T., & Laney, R. (2017). Computer-generated stylistic compositions with long-term repetitive and phrasal structure. Journal of Creative Music Systems, 1(2).

• Conklin, D., and Witten, I. H. (1995). Multiple viewpoint systems for music prediction. Journal of New Music Research, 24(1), 51-73.

• Elmsley, A., Weyde, T., & Armstrong, N. (2017). Generating time: Rhythmic perception, prediction and production with recurrent neural networks. Journal of Creative Music Systems, 1(2).

• Engel, J., Resnick, C., Roberts, A., Dieleman, S., Eck, D., Simonyan, K., & Norouzi, M. (2017). Neural audio synthesis of musical notes with WaveNet autoencoders. https://arxiv.org/abs/1704.01279

• Gjerdingen, R. O. (1989). Using connectionist models to explore complex musical patterns. Computer Music Journal, 13(3), 67-75.

• Gjerdingen, R. (2007). Music in the galant style. New York, NY: Oxford University Press.

• Hadjeres, G., Pachet, F., & Nielsen, F. (2016). Deepbach: A steerable model for Bach chorales generation. arXiv preprint arXiv:1612.01010.

• Huron, D. (2006). Sweet Anticipation. Music and the Psychology of Expectation. Cambridge, MA: MIT Press.

• Janssen, B., Burgoyne, J. A., & Honing, H. (2017). Predicting variation of folk songs: A corpus analysis study on the memorability of melodies. Frontiers in Psychology, 8, 621.

• Janssen, B., van Kranenburg, P., & Volk, A. (2017). Finding occurrences of melodic segments in folk songs employing symbolic similarity measures. Journal of New Music Research, 46(2), 118-134.

• Koelsch, S., Gunter, T. C., Wittfoth, M., & Sammler, D. (2005). Interaction between syntax processing in language and in music: an ERP study. Journal of Cognitive Neuroscience, 17(10), 1565-1577.

• Lerdahl, F., and Jackendoff, R. (1983). "A generative theory of tonal music. Cambridge, MA: MIT Press.

• Margulis, E. H. (2014). On repeat: How music plays the mind. New York, NY: Oxford University Press.

• Meredith, D. (1999). The computational representation of octave equivalence in the Western staff notation system. In Proceedings of the Cambridge Music Processing Colloquium. Cambridge, UK.

• Meredith, D. (2013). COSIATEC and SIATECCompress: Pattern discovery by geometric compression. In Proceedings of the 10th Annual Music Information Retrieval Evaluation eXchange (MIREX'13). Curitiba, Brazil.

• Morgan, E., Fogel, A., Nair, A., & Patel, A. D. (2019). Statistical learning and Gestalt-like principles predict melodic expectations. Cognition, 189, 23-34.

• Pardo, B., & Birmingham, W. P. (2002). Algorithms for chordal analysis. Computer Music Journal, 26(2), 27-49.

• Pearce, M. T., & Wiggins, G. A. (2006). Melody: The influence of context and learning. Music Perception, 23(5), 377–405.

• Raffel, C. (2016). "Learning-based methods for comparing sequences, with applications to audio-to-MIDI alignment and matching". PhD Thesis.

• Ren, I.Y., Koops, H.V, Volk, A., Swierstra, W. (2017). In search of the consensus among musical pattern discovery algorithms. In Proceedings of the International Society for Music Information Retrieval Conference (pp. 671-678). Suzhou, China.

• Roberts, A., Engel, J., Raffel, C., Hawthorne, C., & Eck, D. (2018). A hierarchical latent vector model for learning long-term structure in music. In Proceedings of the International Conference on Machine Learning (pp. 4361-4370). Stockholm, Sweden.

• Rohrmeier, M., & Pearce, M. (2018). Musical syntax I: theoretical perspectives. In Springer Handbook of Systematic Musicology (pp. 473-486). Berlin, Germany: Springer.

• Schellenberg, E. G. (1997). Simplifying the implication-realization model of melodic expectancy. Music Perception, 14(3), 295-318.

• Schmuckler, M. A. (1989). Expectation in music: Investigation of melodic and harmonic processes. Music Perception, 7(2), 109-149.

• Sturm, B.L., Santos, J.F., Ben-Tal., O., & Korshunova, I. (2016), Music transcription modelling and composition using deep learning. In Proceedings of the International Conference on Computer Simulation of Musical Creativity. Huddersfield, UK.

• Temperley, D. (2007). Music and probability. Cambridge, MA: MIT Press.

• Widmer, G. (2017). Getting closer to the essence of music: The con espressione manifesto. ACM Transactions on Intelligent Systems and Technology (TIST), 8(2), 19.