2018:Patterns for Prediction Results

Introduction

THIS PAGE IS UNDER CONSTRUCTION!

The task: ...

Contribution

...

Figure 1. Pattern discovery v segmentation. (A) Bars 1-12 of Mozart’s Piano Sonata in E-flat major K282 mvt.2, showing some ground-truth themes and repeated sections; (B-D) Three linear segmentations. Numbers below the staff in Fig. 1A and below the segmentation in Fig. 1D indicate crotchet beats, from zero for bar 1 beat 1.

For a more detailed introduction to the task, please see 2018:Patterns for Prediction.

Training and Test Datasets

...

Sub code	Submission name	Abstract	Contributors
Task Version	symMono
EN1	Algo name here	PDF	Eric Nichols
FC1	Algo name here	PDF	Florian Colombo
MM	Markov model	N/A	Intended as 'baseline'
Task Version	symPoly
FC1	Algo name here	PDF	Florian Colombo
MM	Markov model	N/A	Intended as 'baseline'

Table 1. Algorithms submitted to Patterns for Prediction 2018.

Results

Next to testing how well different algorithms compare when measured with the metrics introduced in earlier forms of this track, the goal of this year's run of drts was also to investigate alternative evaluation measures. Next to establishment, occurrence and three-layer measures, which determine the success of an algorithm to find annotated patterns, we also evaluated coverage and lossless compression of the algorithms, i.e., to what extent a piece is covered, or can be compressed, by discovered patterns.

(For mathematical definitions of the various metrics, please see 2017:Discovery_of_Repeated_Themes_&_Sections#Evaluation_Procedure.)

SymMono

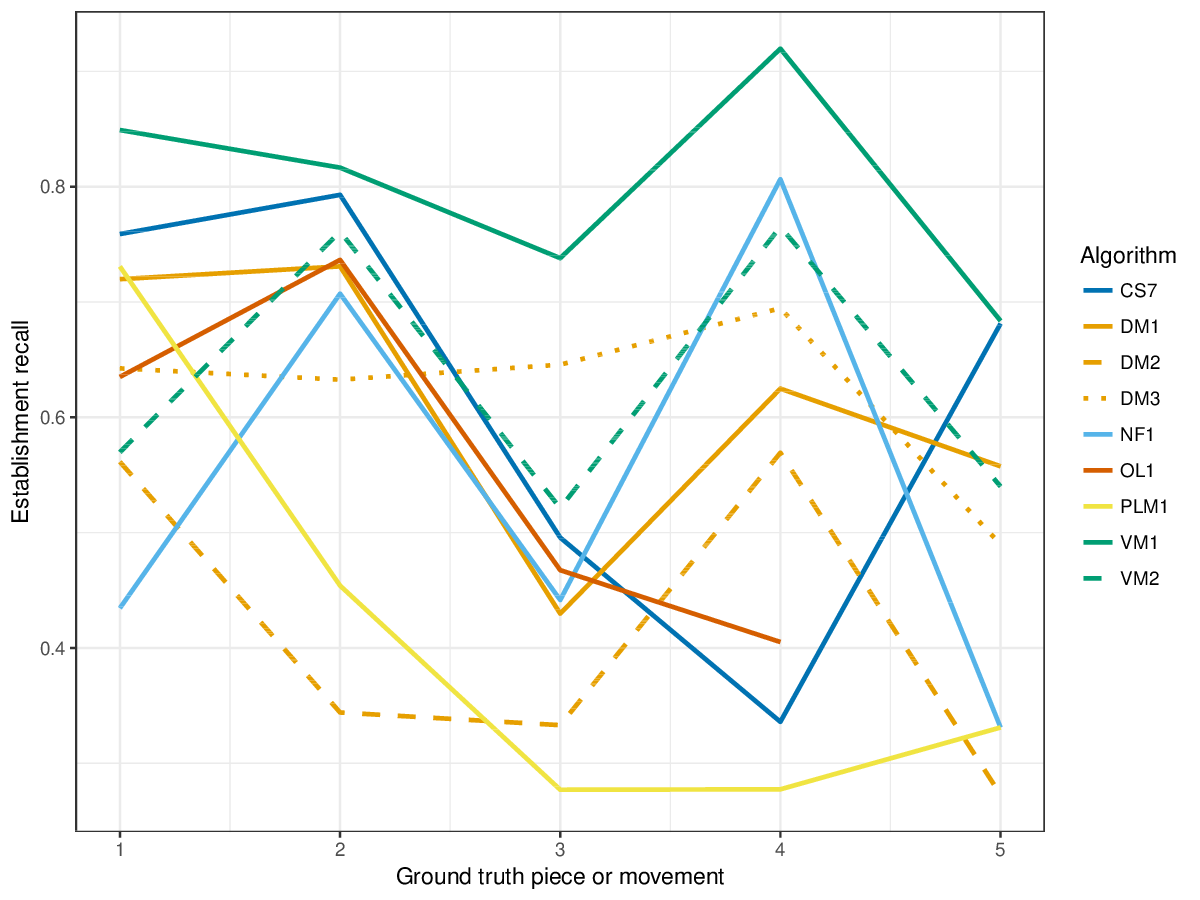
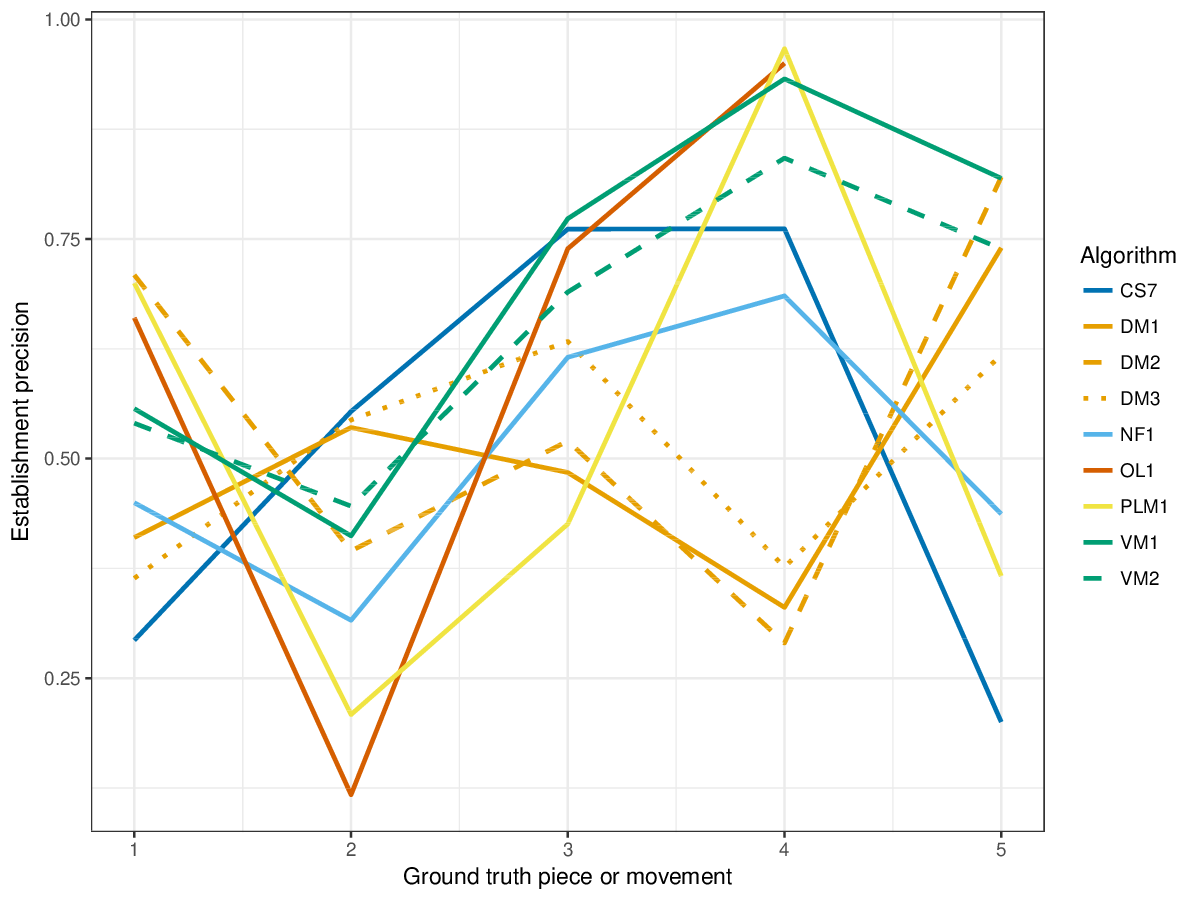
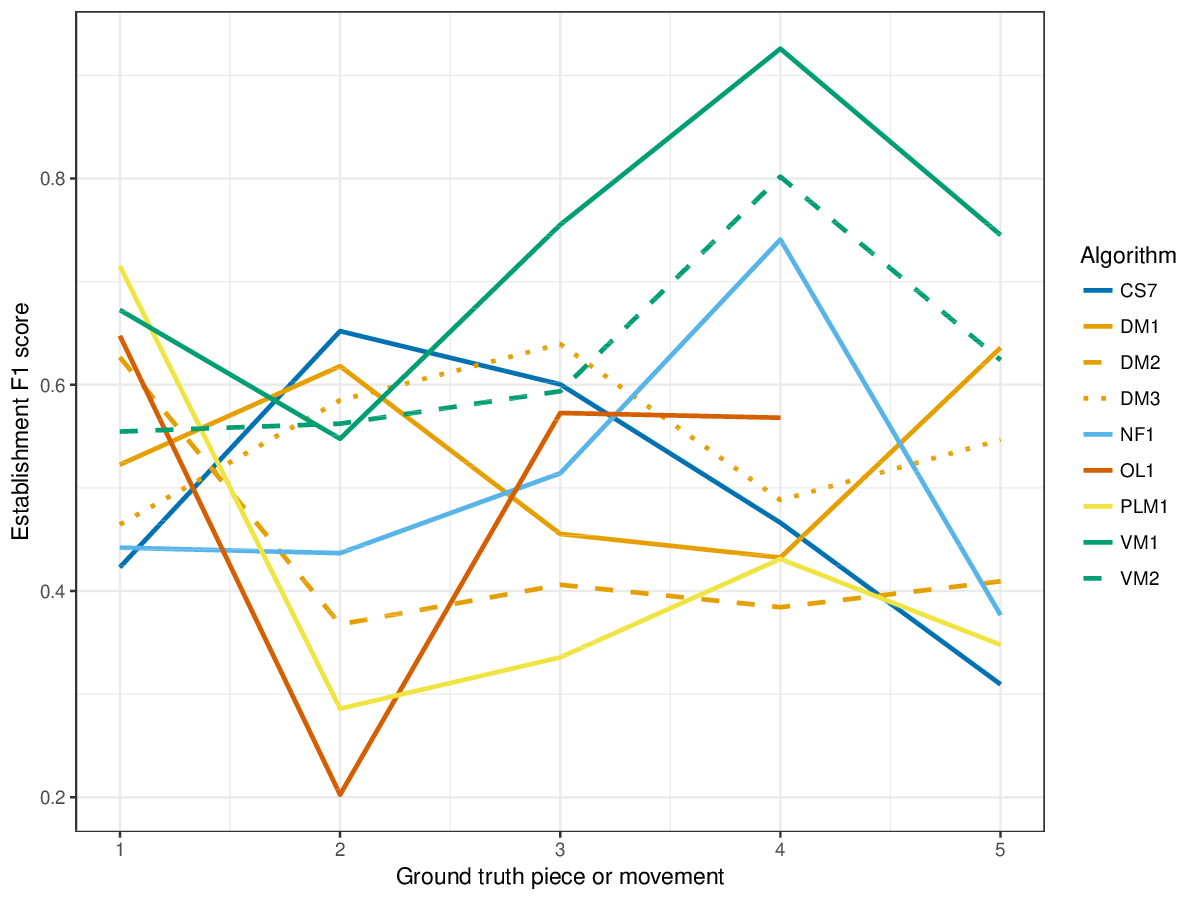
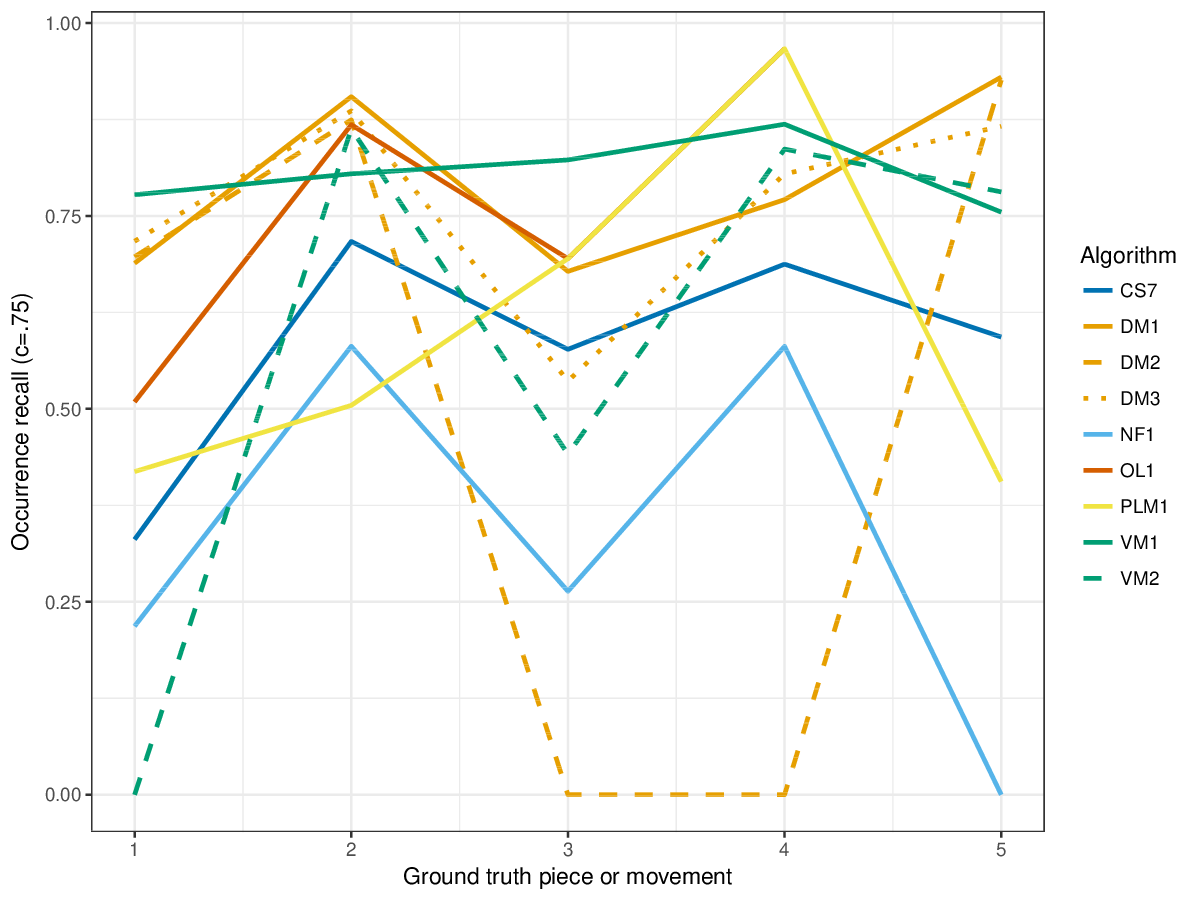
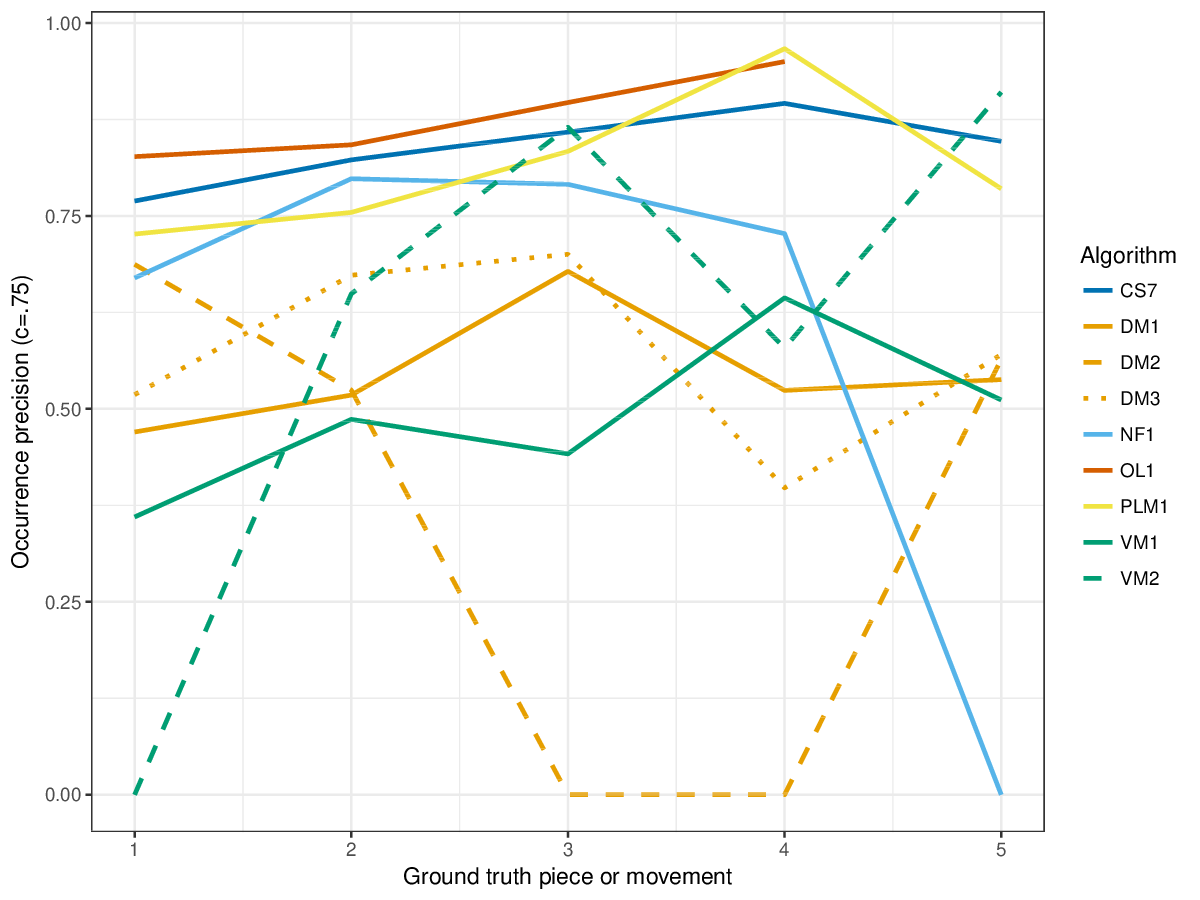
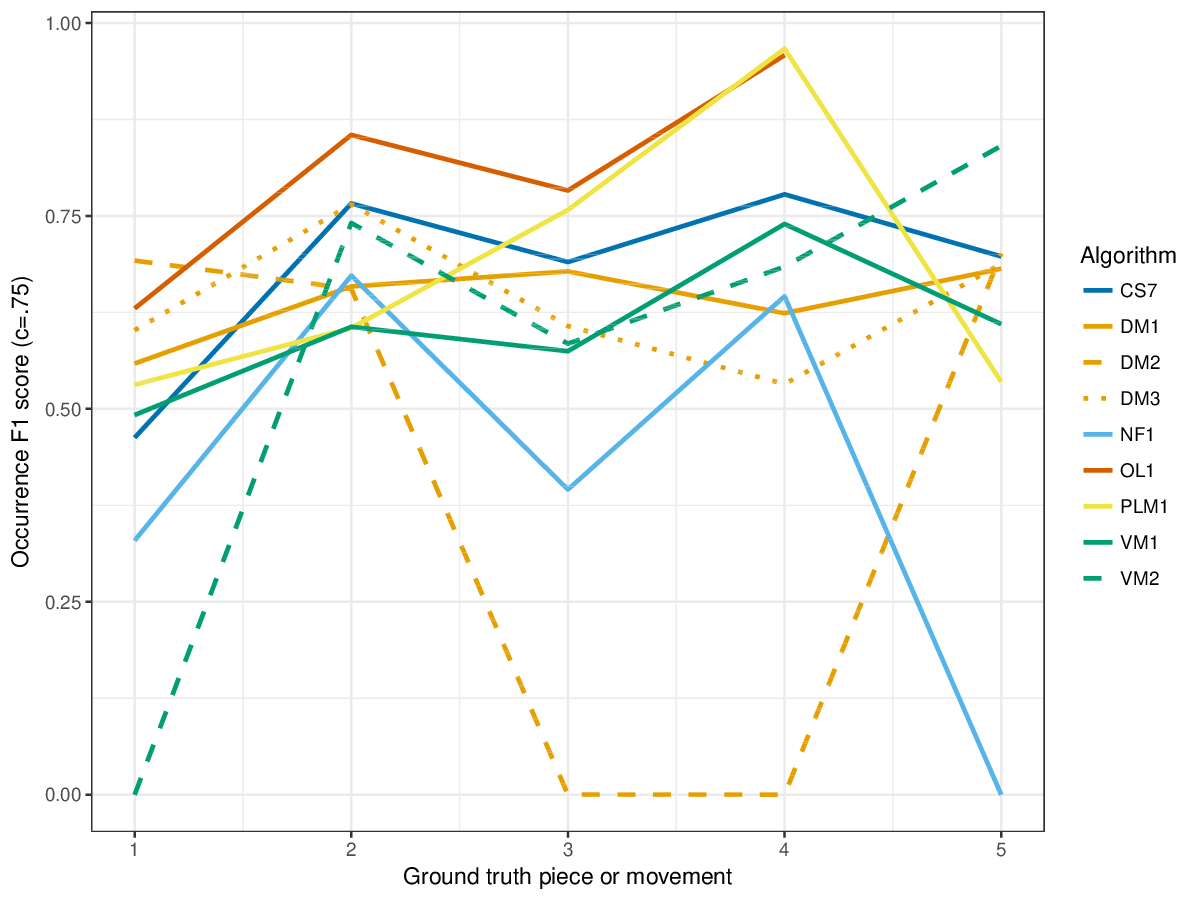
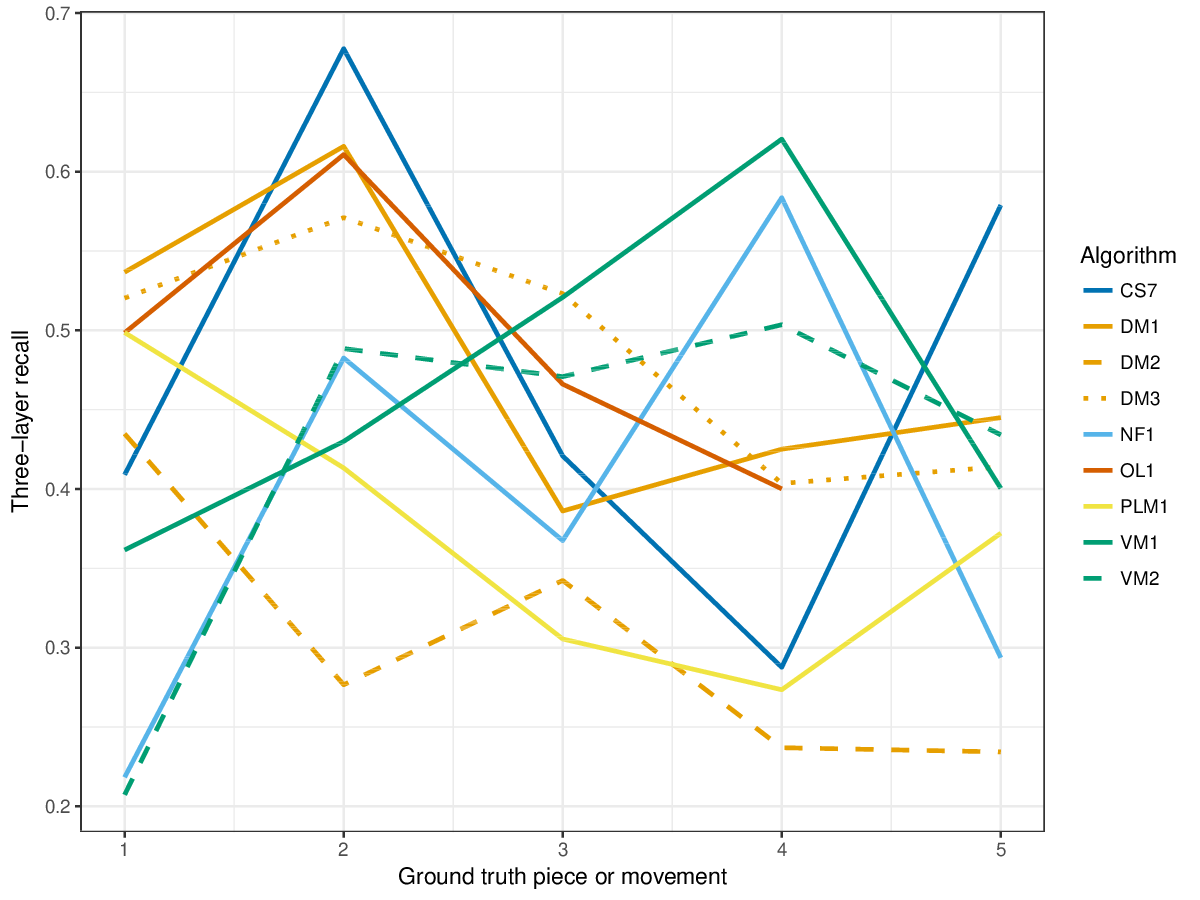
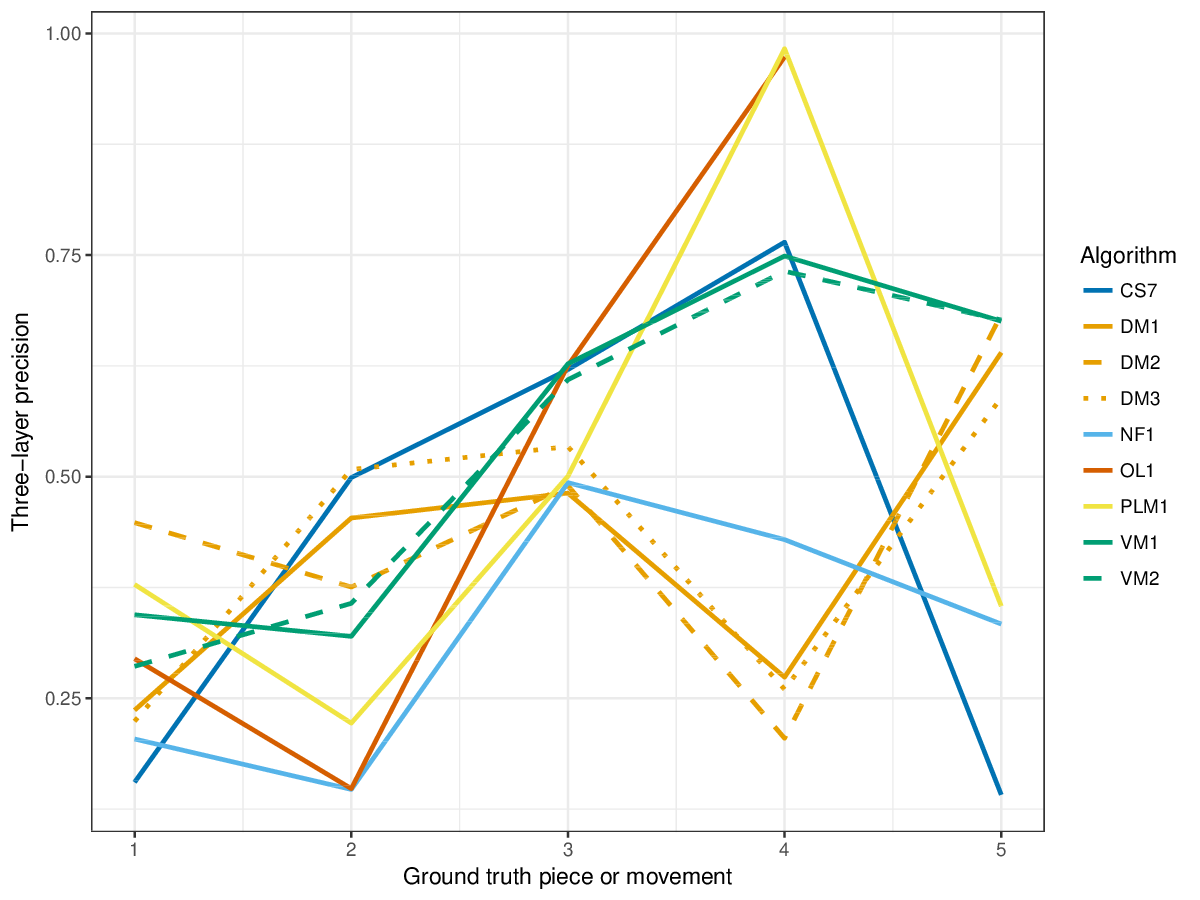
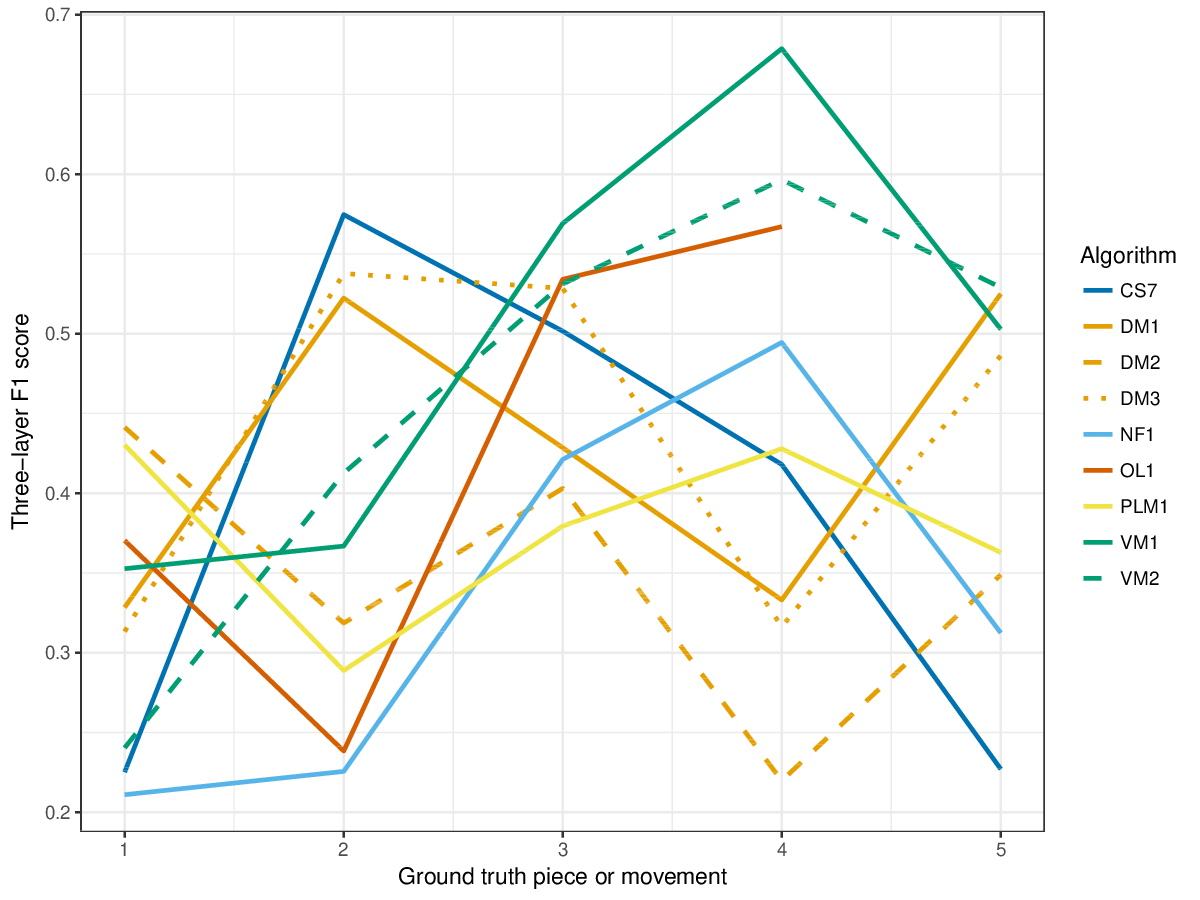
VM1, successful in the last years' editions of drts, achieves overall highest results for the establishment metrics (cf. Figures 1-3), i.e., it finds a great number of the annotated patterns. It is only outperformed by other measures on piece 2 of the ground truth, where DM1 and DM3, and the new entry CS7 achieve higher results for establishment F1 score. CS7 is overall successful with respect to finding occurrences of patterns (cf. Figures 4-6), comparable to successful results of previous years. (NB: OL1 did not run on piece 5 of the ground truth, which is why values are missing.) The three-layer measures (Figures 7-9) show varying degrees of agreement with the ground truth for the ground truth pieces, and again CS7 and VM1 compare favourably to previous submissions.

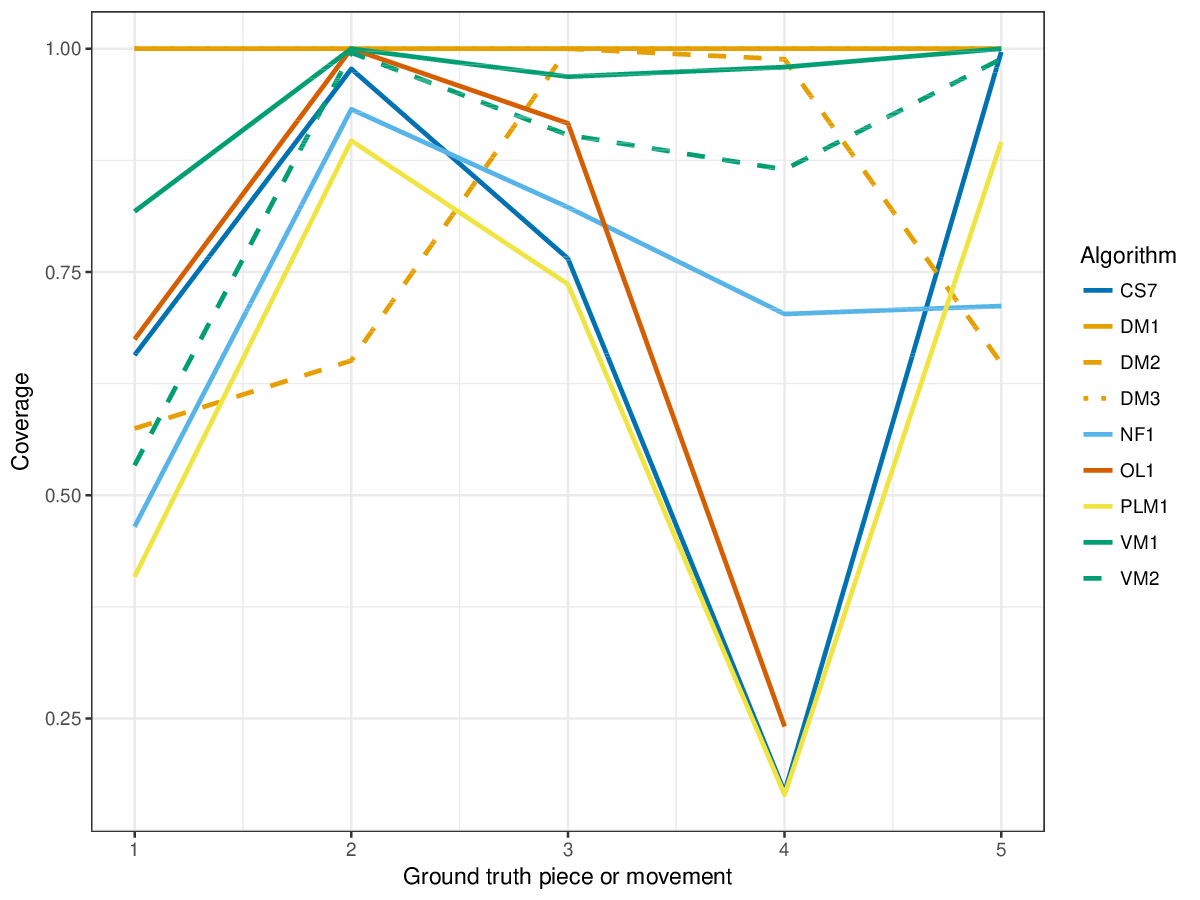
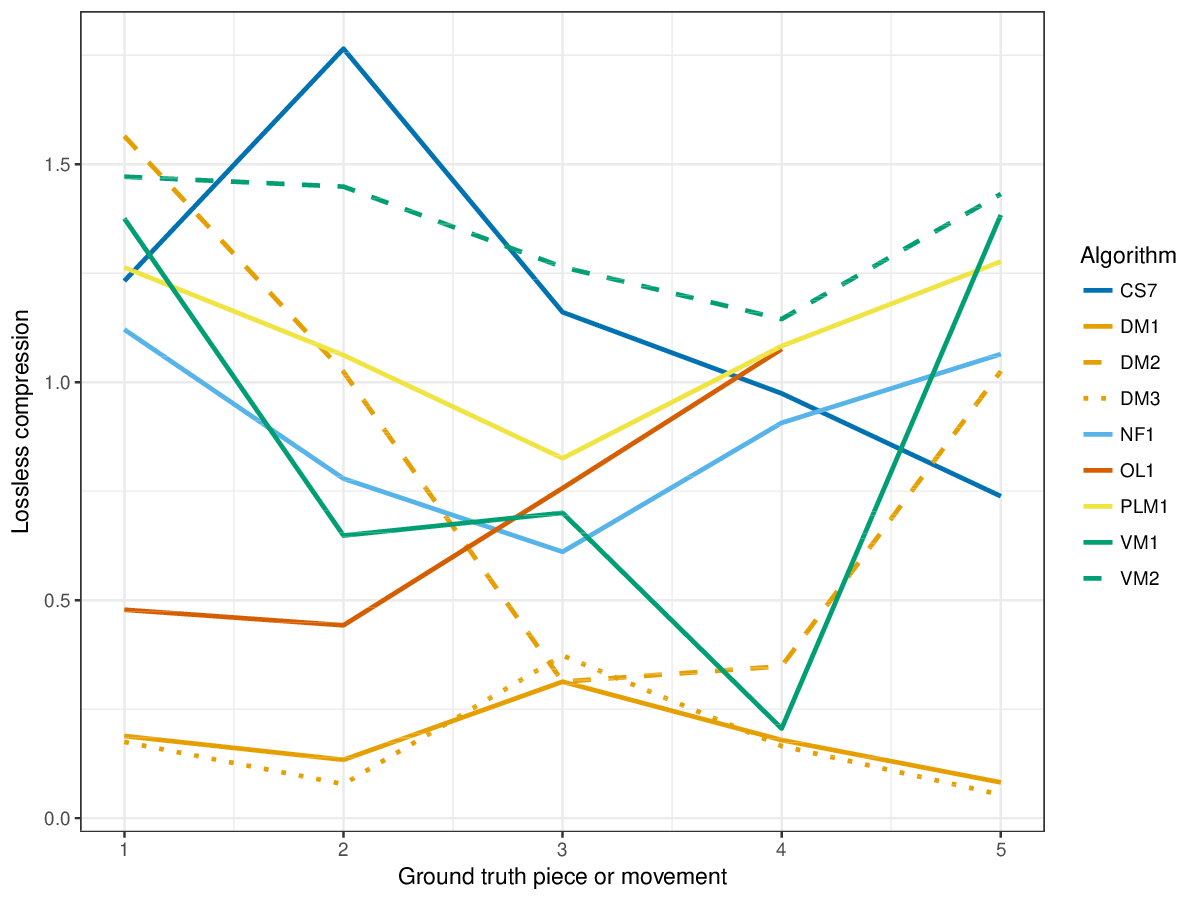
The new measure coverage shows that VM1, DM1 and DM3 find patterns in almost all notes of the ground truth pieces (cf. Figure 10); other algorithms share this tendency for piece 2 and 5 of the ground truth, but in other pieces, most notably piece 4, CS7 and other algorithms seem to have a very sparse coverage of the piece with patterns. An abundance of overlapping patterns lead to poor lossless compression scores, and CS7 seems to find few overlapping patterns, as its score at lossless compression is overall highest (cf. Figure 11), notably also for piece 2 where it achieved high coverage, too: this means that it found most notes of the piece as patterns, and these patterns can be used to compress the piece very successfully.

Runtimes were not evaluated this year, as the comparison of the machines of new submissions to runtimes from previous years would not have been very conclusive. The new submission, CS7, completed analysis of the ground truth pieces in a few minutes on a 2 GHz Intel Core i5 machine.

SymPoly

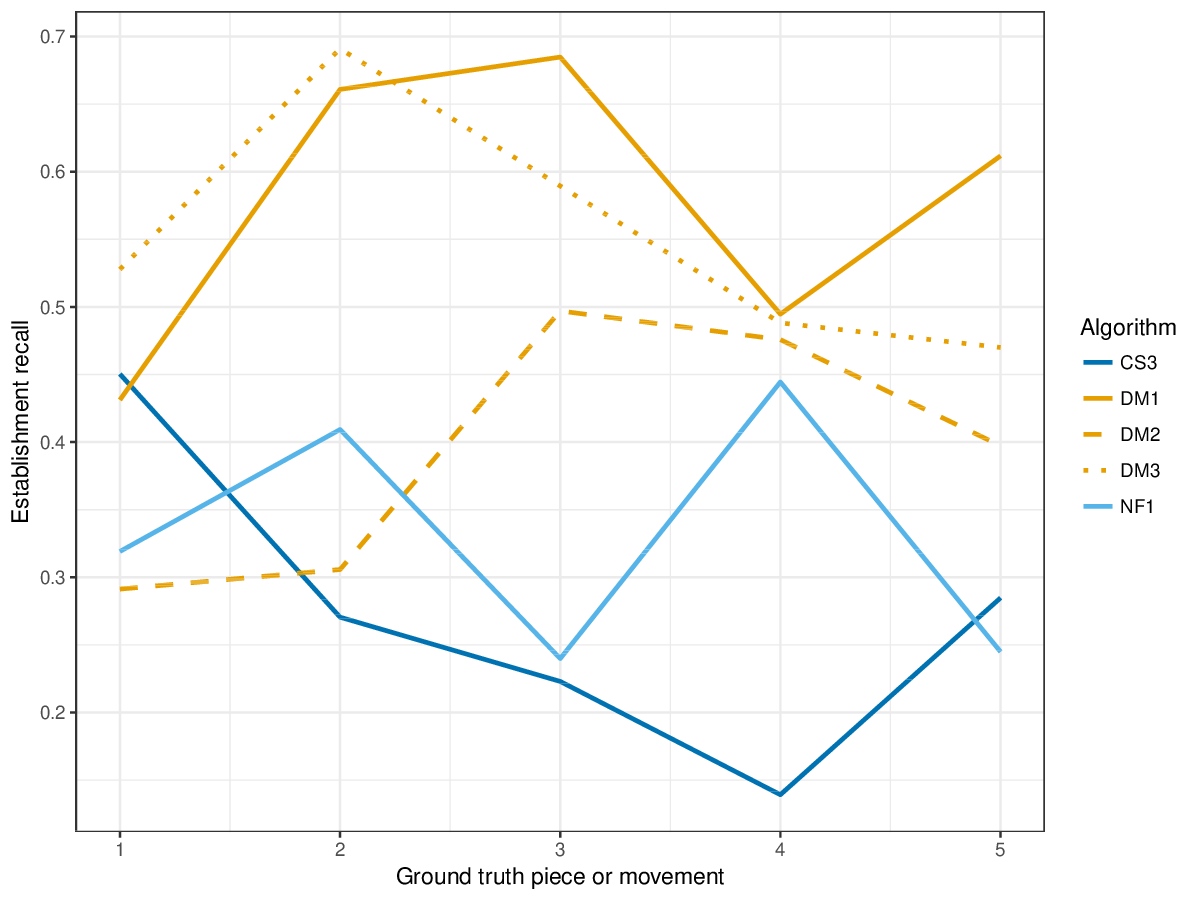
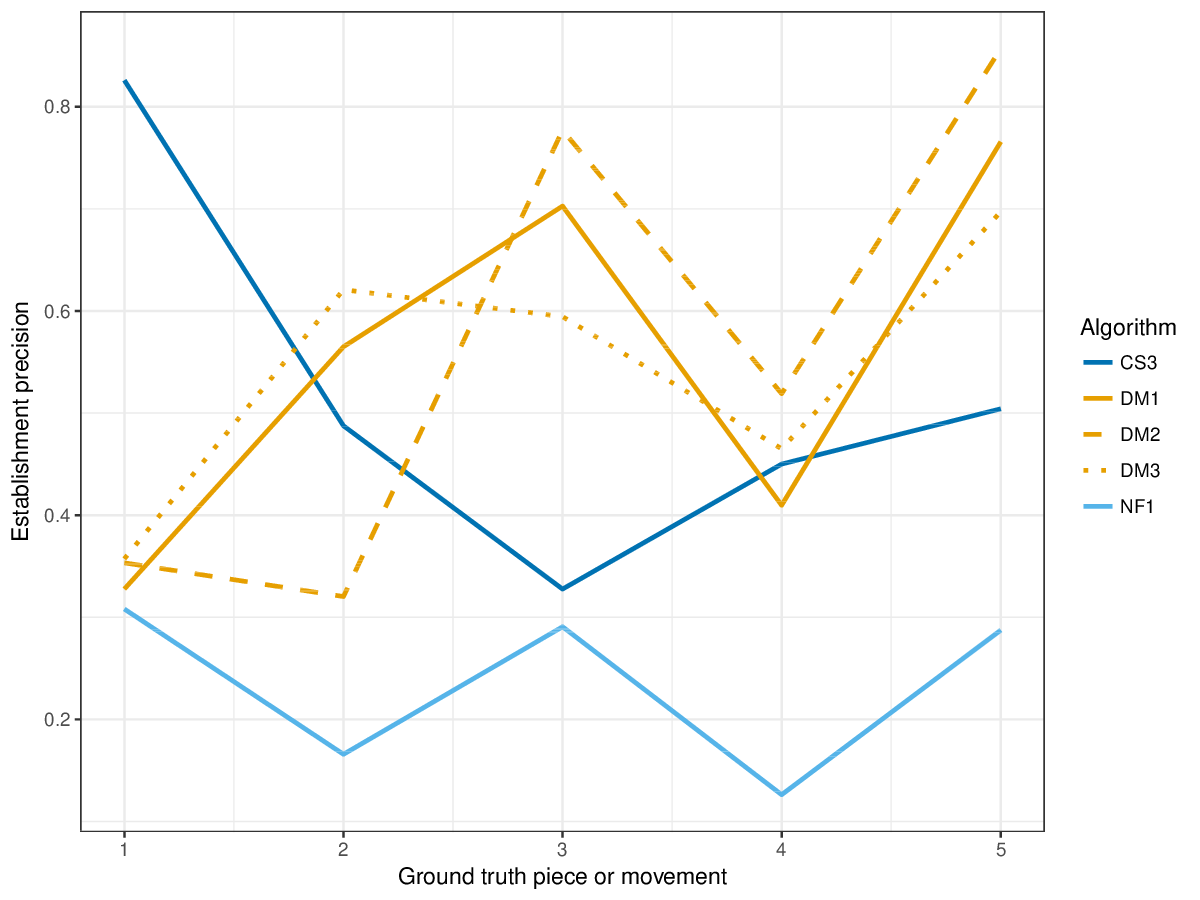
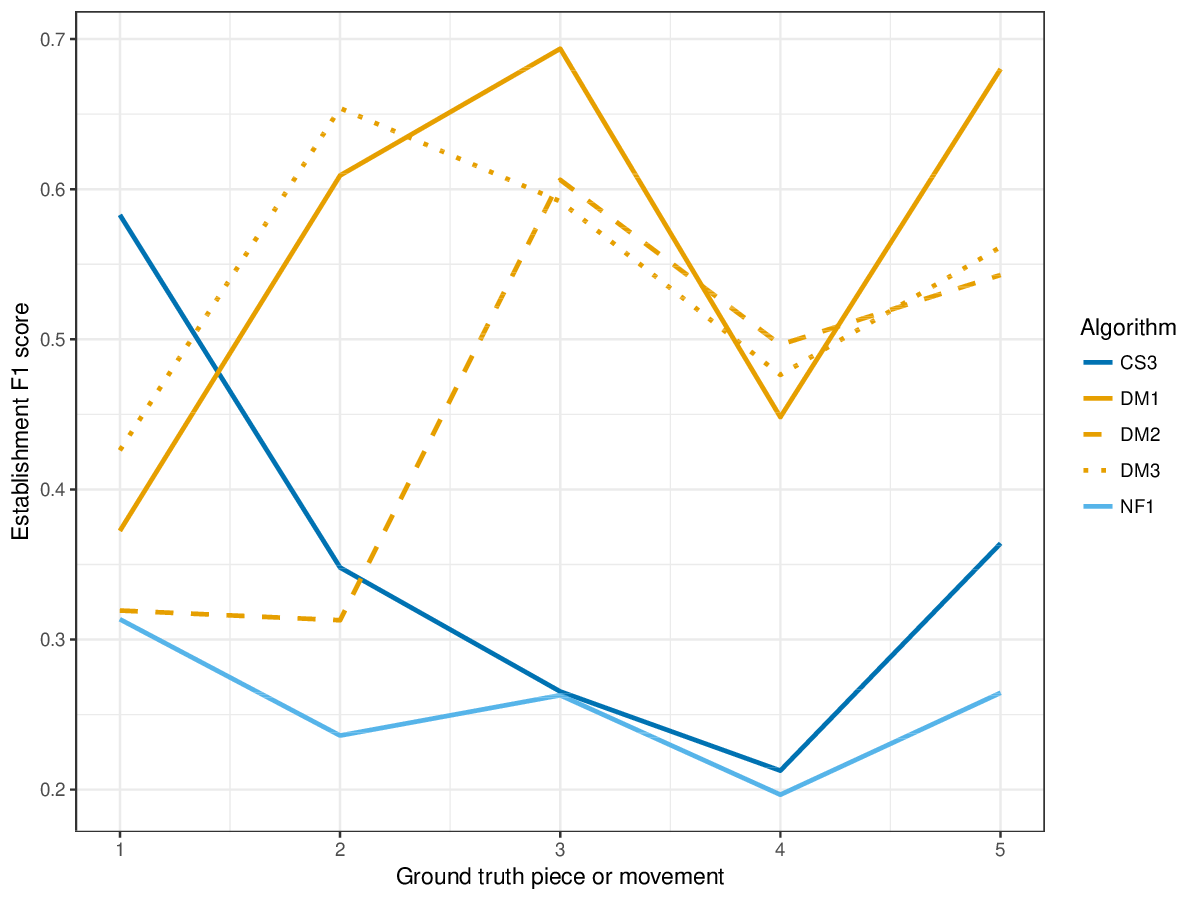
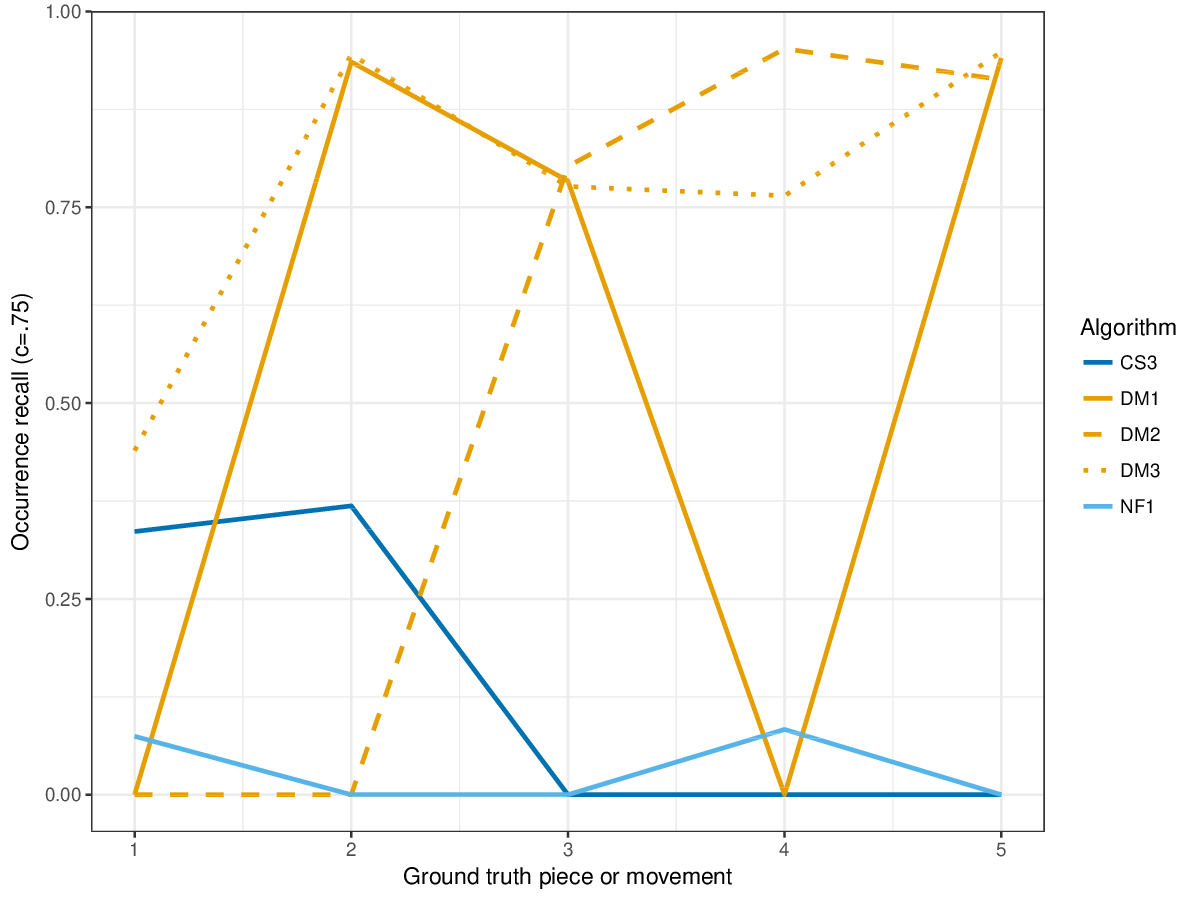
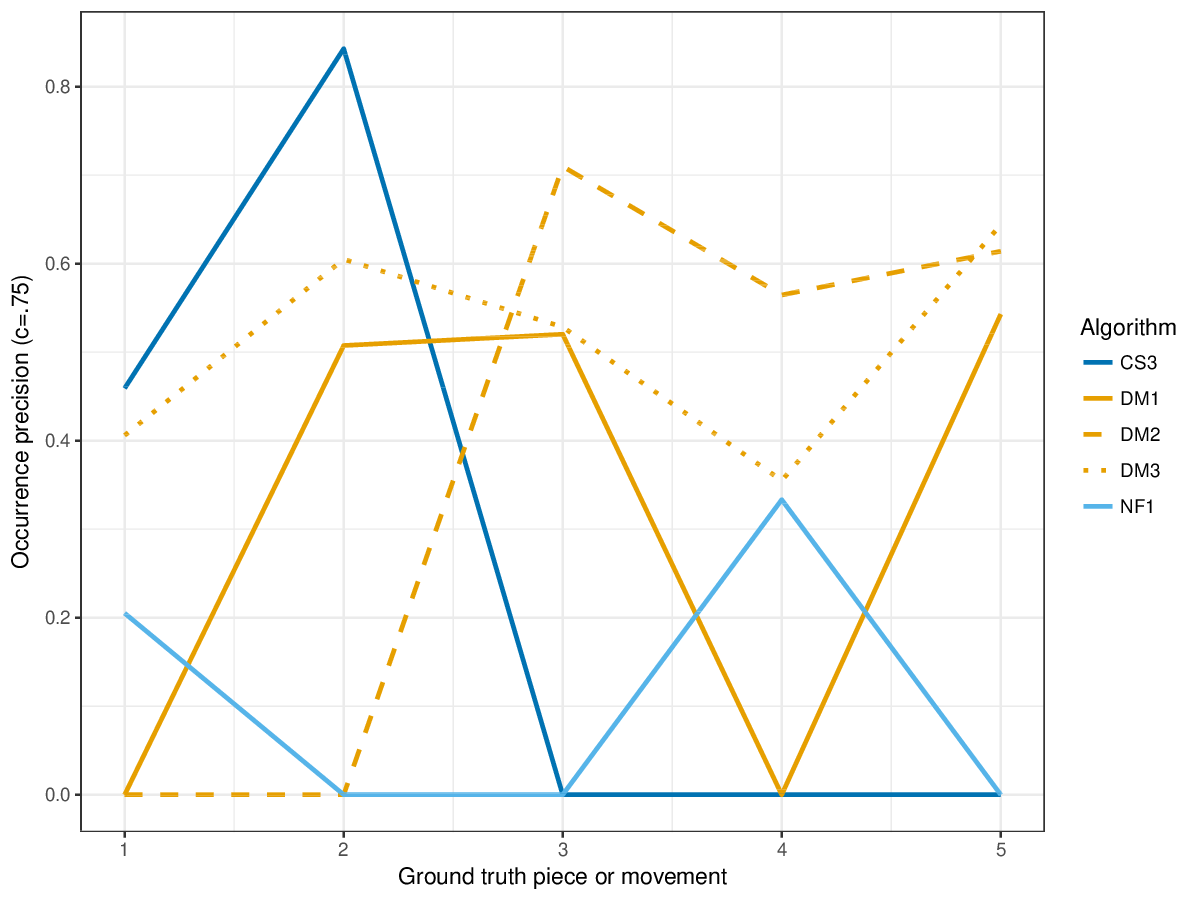
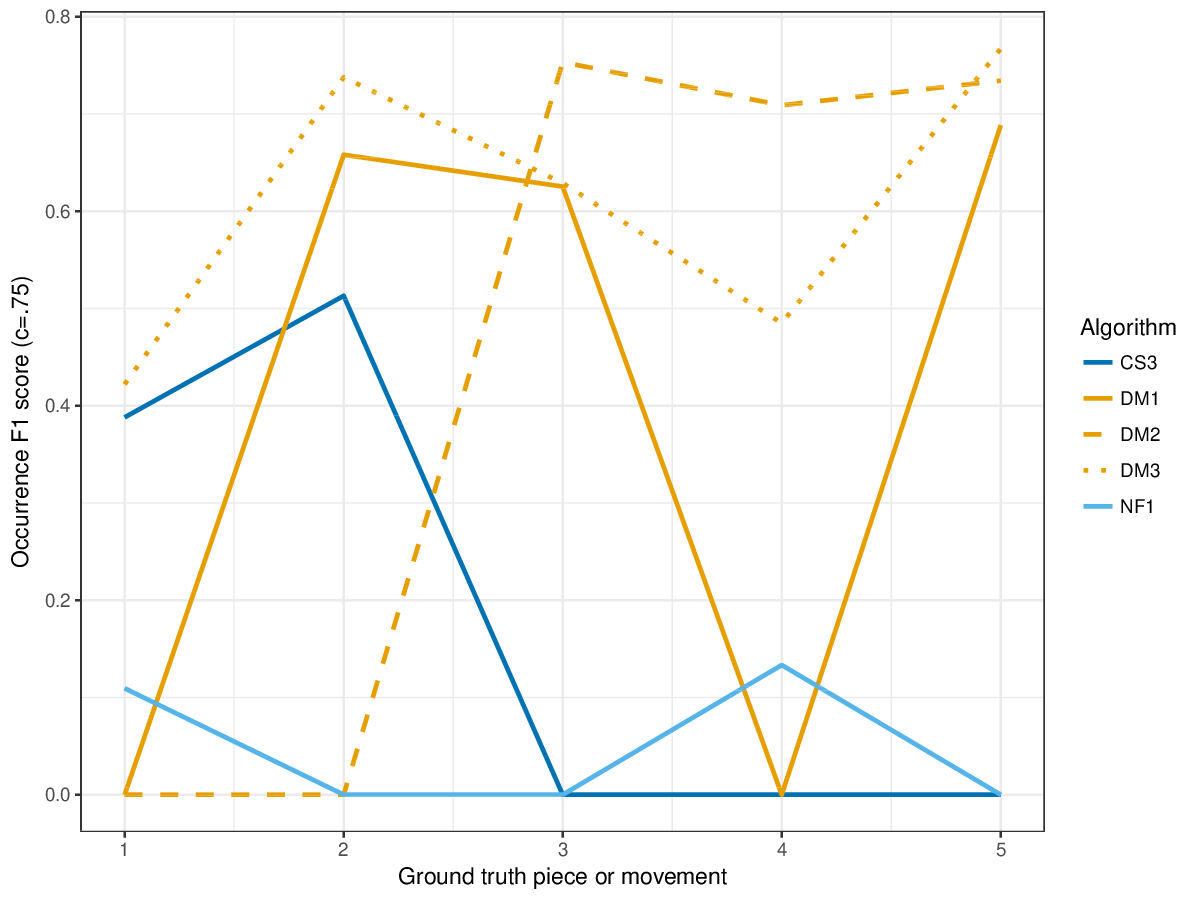
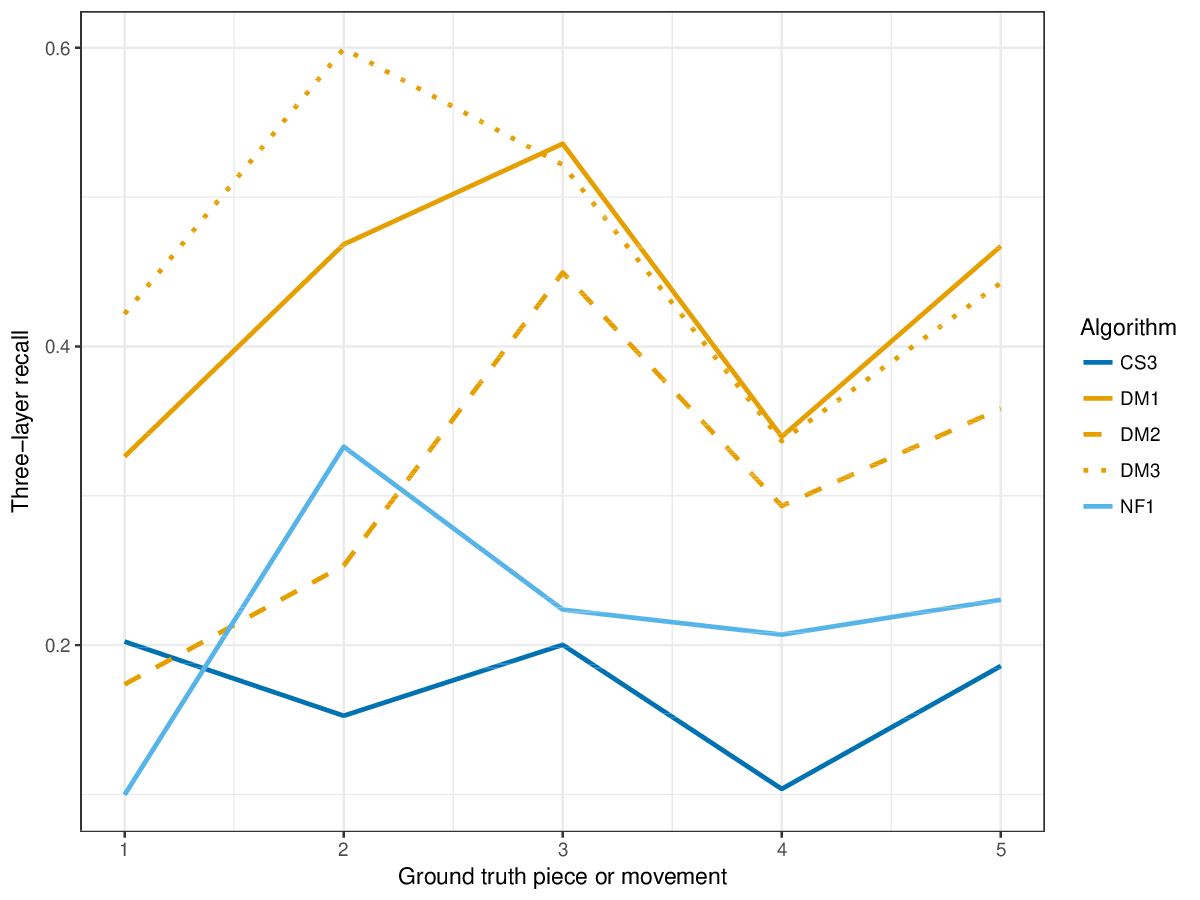
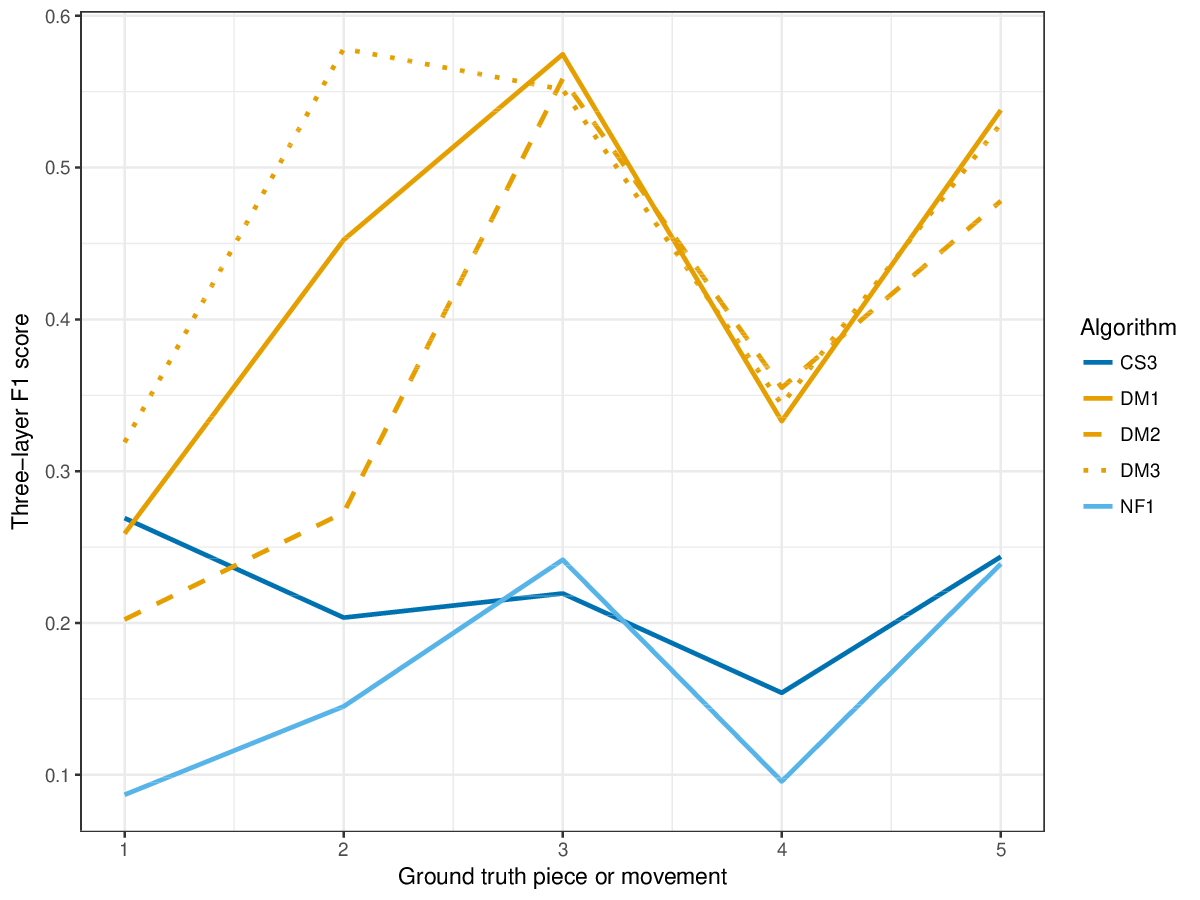
DM1, the most successful measure for polyphonic discovery, again compares favourably in the establishment, occurrence and three-layer metrics this year. The new submission, CS3, outperforms DM1-DM3 in piece 1 on establishment measures (cf. Figures 12-14) , and in piece 2 on occurrence precision (cf. Figure 15).

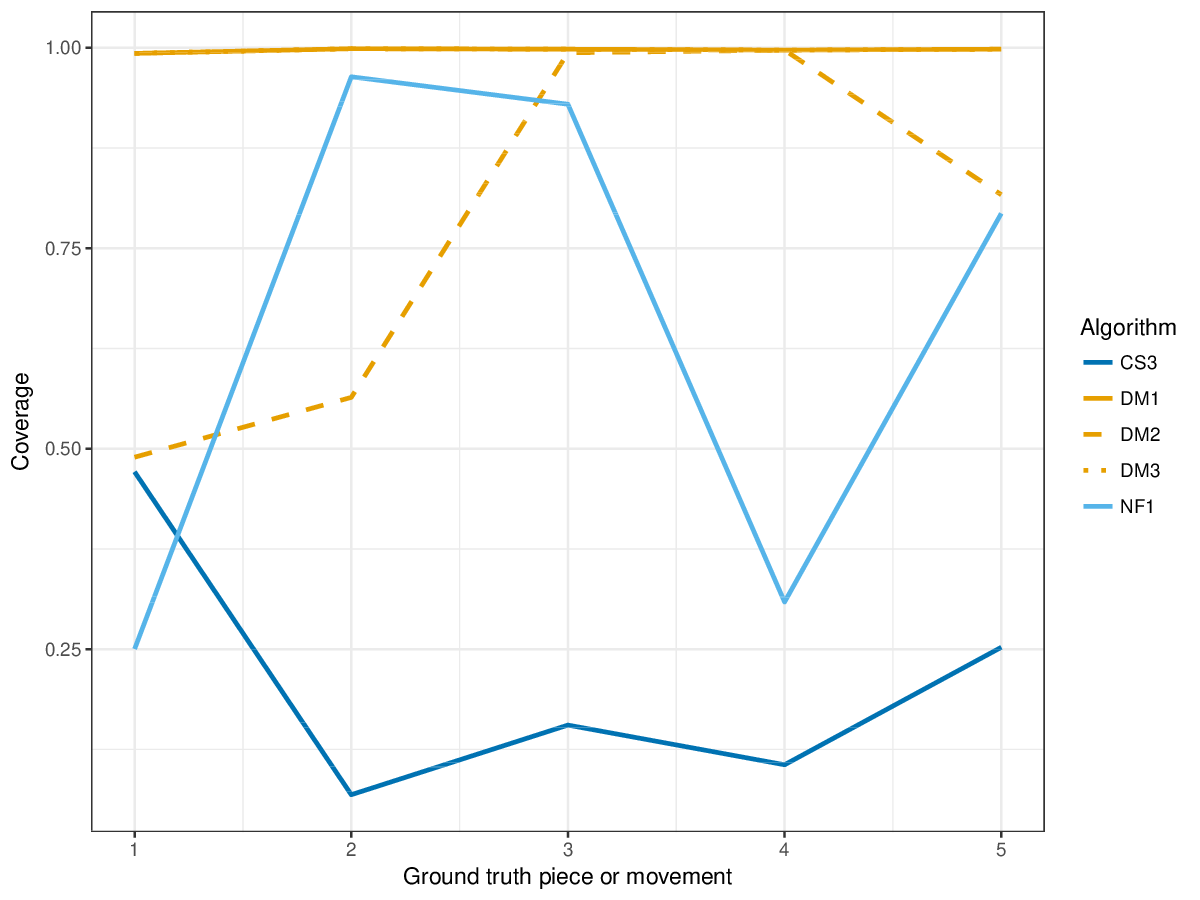
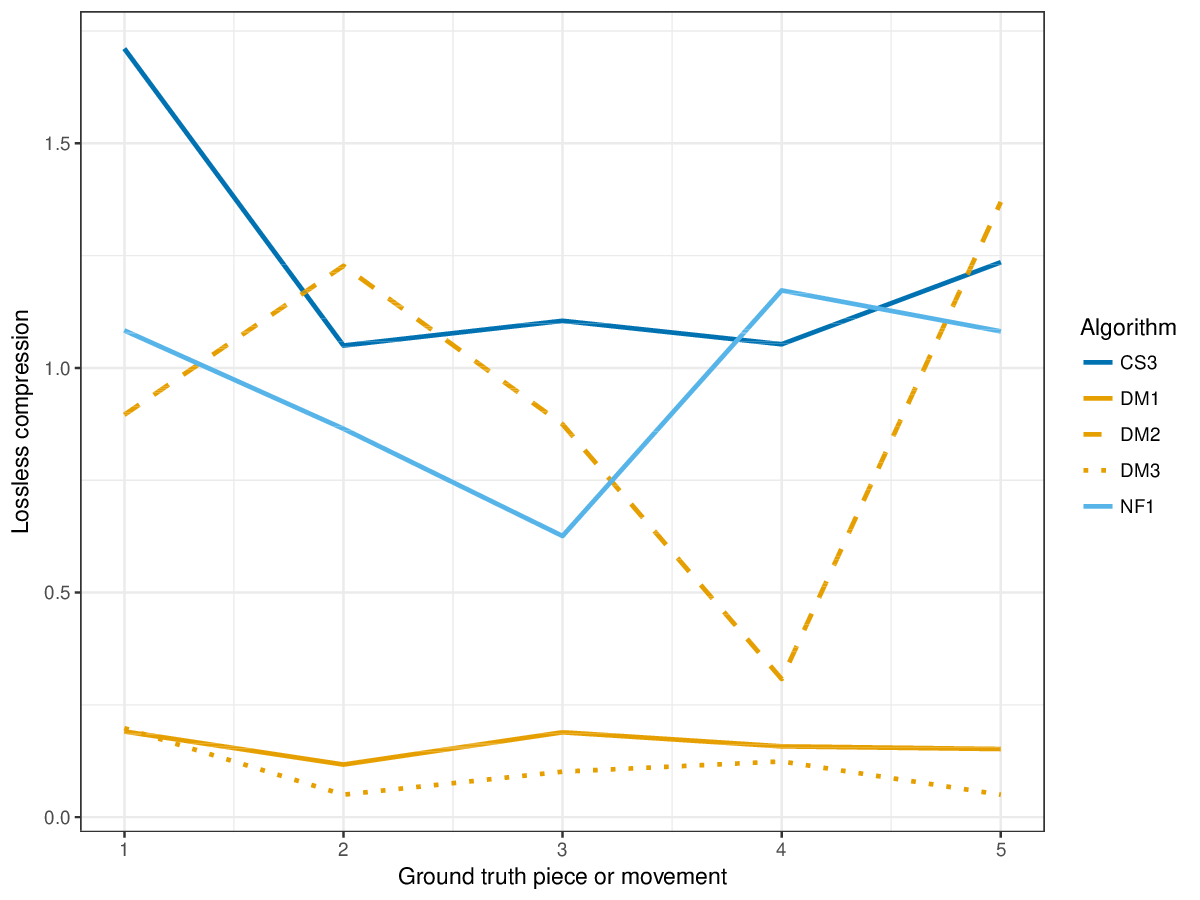
Coverage shows again that DM1 and DM3 find patterns in almost all notes of the ground truth pieces (Figure 21). CS3, NF1 and DM2 (which was optimized for precision metrics) show lower coverage, CS3 lowest overall. CS3 achieves overall highest values in lossless compression (Figure 22).

Runtimes were not evaluated this year, as the comparison of the machines of new submissions to runtimes from previous years would not have been very conclusive. The new submission, CS3, completed analysis of the ground truth pieces in a few minutes on a 2 GHz Intel Core i5 machine.

Discussion

The new compression evaluation measures are not highly correlated with the metrics measuring retrieval of annotated patterns. This may be caused by the fact that lossless compression is lower for algorithms which find overlapping patterns: human annotators, and also some pattern discovery algorithms, may find valid overlapping patterns, as patterns may be hierarchically layered (e.g., motifs which are part of themes). We will add new, prediction based measures, and new ground truth pieces to the task next year.

Berit Janssen, Iris Ren, Tom Collins, Anja Volk.

Figures

SymMono

Figure 1. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

Figure 2. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?

Figure 3. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.

Figure 4. Occurrence recall ($c=.75$) averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

Figure 5. Occurrence precision ($c=.75$) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?

Figure 6. Occurrence F1 ($c=.75$) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.

Figure 7. Three-layer recall averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment recall), three-layer recall uses $2|P\cap Q|/(|P|+|Q|)$, which is a kind of F1 measure.

Figure 8. Three-layer precision averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment precision), three-layer precision uses $2|P\cap Q|/(|P|+|Q|)$, which is a kind of F1 measure.

Figure 9. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.

Figure 10. Coverage of the discovered patterns of each piece/movement. Coverage measures the fraction of notes of a piece covered by discovered patterns.

Figure 11. Lossless compression achieved by representing each piece/movement in terms of patterns discovered by a given algorithm. Next to patterns and their repetitions, also the uncovered notes are represented, such that the complete piece could be reconstructed from the compressed representation.

SymPoly

Figure 12. Establishment recall averaged over each piece/movement. Establishment recall answers the following question. On average, how similar is the most similar algorithm-output pattern to a ground-truth pattern prototype?

Figure 13. Establishment precision averaged over each piece/movement. Establishment precision answers the following question. On average, how similar is the most similar ground-truth pattern prototype to an algorithm-output pattern?

Figure 14. Establishment F1 averaged over each piece/movement. Establishment F1 is an average of establishment precision and establishment recall.

Figure 15. Occurrence recall ($c=.75$) averaged over each piece/movement. Occurrence recall answers the following question. On average, how similar is the most similar set of algorithm-output pattern occurrences to a discovered ground-truth occurrence set?

Figure 16. Occurrence precision ($c=.75$) averaged over each piece/movement. Occurrence precision answers the following question. On average, how similar is the most similar discovered ground-truth occurrence set to a set of algorithm-output pattern occurrences?

Figure 17. Occurrence F1 ($c=.75$) averaged over each piece/movement. Occurrence F1 is an average of occurrence precision and occurrence recall.

Figure 18. Three-layer recall averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment recall), three-layer recall uses $2|P\cap Q|/(|P|+|Q|)$, which is a kind of F1 measure.

600px

Figure 19. Three-layer precision averaged over each piece/movement. Rather than using $|P\cap Q|/\max\{|P|,|Q|\}$ as a similarity measure (which is the default for establishment precision), three-layer precision uses $2|P\cap Q|/(|P|+|Q|)$, which is a kind of F1 measure.

Figure 20. Three-layer F1 (TLF) averaged over each piece/movement. TLF is an average of three-layer precision and three-layer recall.

Figure 21. Coverage of the discovered patterns of each piece/movement. Coverage measures the fraction of notes of a piece covered by discovered patterns.

Figure 22. Lossless compression achieved by representing each piece/movement in terms of patterns discovered by a given algorithm. Next to patterns and their repetitions, also the uncovered notes are represented, such that the complete piece could be reconstructed from the compressed representation.

Tables

SymMono

Click to download SymMono pattern retrieval results table

Click to download SymMono compression results table

SymPoly

Click to download SymPoly pattern retrieval results table

Click to download SymPoly compression results table