2018:Patterns for Prediction Results
Contents
Introduction
In brief:
We look for
(1) Algorithms that take an excerpt of music as input (the prime), and output a predicted continuation of the excerpt.
(2) Additionally or alternatively, algorithms that take a prime and one or more continuations as input, and output the likelihood that each continuation is the genuine extension of the prime.
In more detail: One facet of human nature comprises the tendency to form predictions about what will happen in the future (Huron, 2006). Music, consisting of complex temporally extended sequences, provides an excellent setting for the study of prediction, and this topic has received attention from fields including but not limited to psychology (Collins, Tillmann, et al., 2014; Janssen, Burgoyne and Honing, 2017; Schellenberg, 1997; Schmukler, 1989), neuroscience (Koelsch et al., 2005), music theory (Gjerdingen, 2007; Lerdahl & Jackendoff, 1983; Rohrmeier & Pearce, 2018), music informatics (Conklin & Witten, 1995; Cherla et al., 2013), and machine learning (Elmsley, Weyde, & Armstrong, 2017; Hadjeres, Pachet, & Nielsen, 2016; Gjerdingen, 1989; Roberts et al., 2018; Sturm et al., 2016). In particular, we are interested in the way exact and inexact repetition occurs over the short, medium, and long term in pieces of music (Margulis, 2014; Widmer, 2016), and how these repetitions may interact with "schematic, veridical, dynamic, and conscious" expectations (Huron, 2006) in order to form a basis for successful prediction.
We call for algorithms that may model such expectations so as to predict the next musical events based on given, foregoing events (the prime). We invite contributions from all fields mentioned above (not just pattern discovery researchers), as different approaches may be complementary in terms of predicting correct continuations of a musical excerpt. We would like to explore these various approaches to music prediction in a MIREX task. For subtask (1) above (see "In brief"), the development and test datasets will contain an excerpt of a piece up until a cut-off point, after which the algorithm is supposed to generate the next N musical events up until 10 quarter-note beats, and we will quantitatively evaluate the extent to which an algorithm's continuation corresponds to the genuine continuation of the piece. For subtask (2), in addition to containing a prime, the development and test datasets will also contain continuations of the prime, one of which will be genuine, and the algorithm should rate the likelihood that each continuation is the genuine extension of the prime, which again will be evaluated quantitatively.
What is the relationship between pattern discovery and prediction? The last five years have seen an increasing interest in algorithms that discover or generate patterned data, leveraging methods beyond typical (e.g., Markovian) limits (Collins & Laney, 2017; MIREX Discovery of Repeated Themes & Sections task; Janssen, van Kranenburg and Volk, 2017; Ren et al., 2017; Widmer, 2016). One of the observations to emerge from the above-mentioned MIREX pattern discovery task is that an algorithm that is "good" at discovering patterns ought to be extendable to make "good" predictions for what will happen next in a given music excerpt (Meredith, 2013). Furthermore, evaluating the ability to predict may provide a stronger (or at least complementary) evaluation of an algorithm's pattern discovery capabilities, compared to evaluating its output against expert-annotated patterns, where the notion of "ground truth" has been debated (Meredith, 2013).
Contribution
...
For a more detailed introduction to the task, please see 2018:Patterns for Prediction.
Datasets and Algorithms
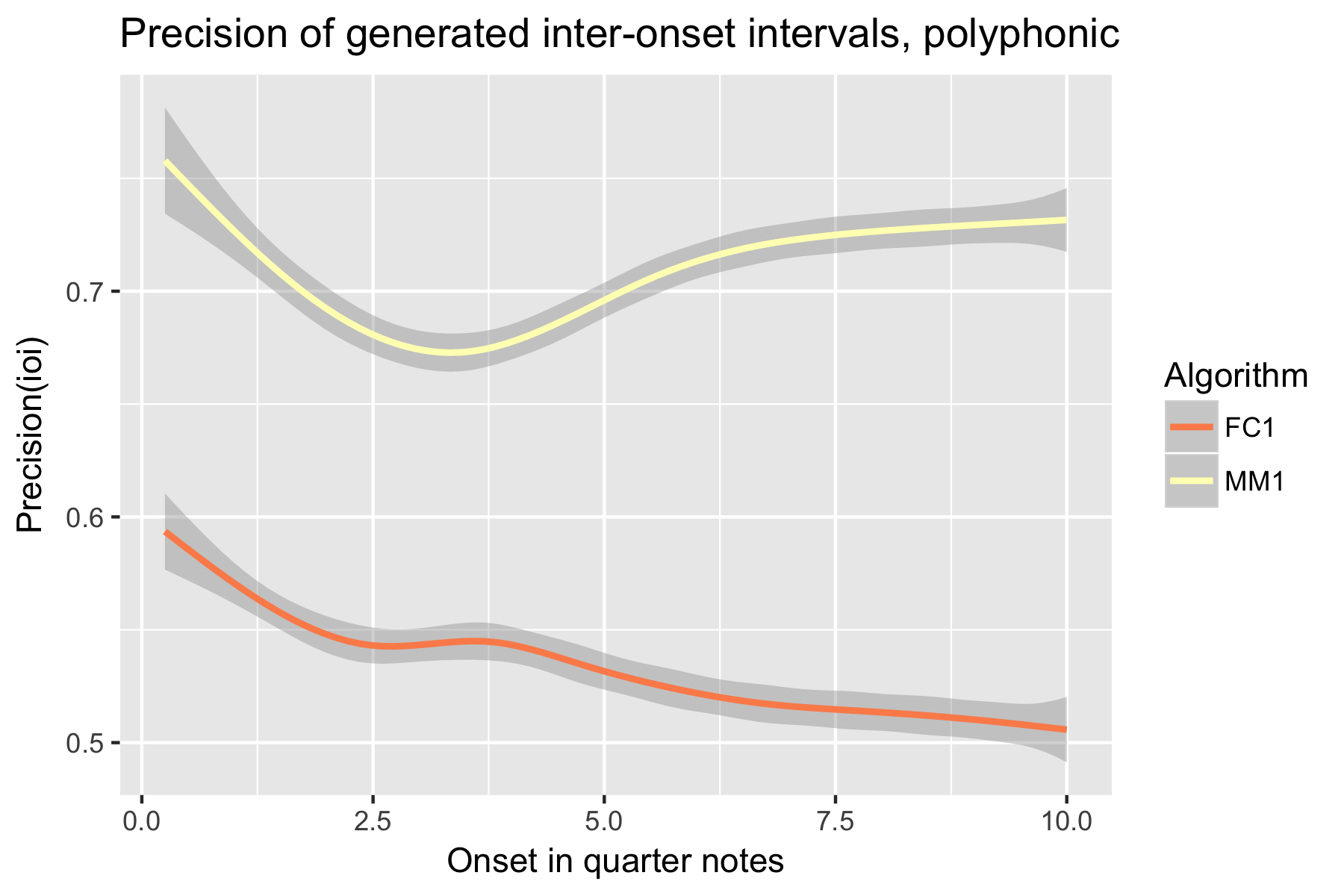
The Patterns for Prediction Development Dataset (PPDD-Jul2018) has been prepared by processing a randomly selected subset of the Lakh MIDI Dataset (LMD, Raffel, 2016). It has audio and symbolic versions crossed with monophonic and polyphonic versions. The audio is generated from the symbolic representation, so it is not "expressive". The symbolic data is presented in CSV format. For example,
20,64,62,0.5,0 20.66667,65,63,0.25,0 21,67,64,0.5,0 ...
would be the start of a prime where the first event had ontime 20 (measured in quarter-note beats -- equivalent to bar 6 beat 1 if the time signature were 4-4), MIDI note number (MNN) 64, estimated morphetic pitch number 62 (see p. 352 from Collins, 2011 for a diagrammatic explanation; for more details, see Meredith, 1999), duration 0.5 in quarter-note beats, and channel 0. Re-exports to MIDI are also provided, mainly for listening purposes. We also provide a descriptor file containing the original Lakh MIDI Dataset id, the BPM, time signature, and a key estimate. The audio dataset contains all these files, plus WAV files. Therefore, the audio and symbolic variants are identical to one another, apart from the presence of WAV files. All other variants are non-identical, although there may be some overlap, as they were all chosen from LMD originally.
The provenance of the Patterns for Prediction Test Dataset (PPTD) will not be disclosed, but it shares simiarlity with LMD and not from LMD, if you are concerned about overfitting.
There are small (100 pieces), medium (1,000 pieces), and large (10,000 pieces) variants of each dataset, to cater to different approaches to the task (e.g., a point-set pattern discovery algorithm developer may not want/need as many training examples as a neural network researcher). Each prime lasts approximately 35 sec (according to the BPM value in the original MIDI file) and each continuation covers the subsequent 10 quarter-note beats. We would have liked to provide longer primes (as 35 sec affords investigation of medium- but not really long-term structure), but we have to strike a compromise between ideal and tractable scenarios.
Submissions to the symMono and symPoly variants of the tasks are listed in Table 1. There were no submissions to the audMono or audPoly variants of the tasks this year. The task captains prepared a first-order Markov model (MM) over a state space of measure beat and key-centralized MIDI note number. This enabled evaluation of the implicit subtask, and can also serve as a point of comparison for the explicit task. It should be noted, however, that this model had access to the full song/piece – not just the prime – so it is at an advantage compared to EN1 and FC1 in the explicit task.
| Sub code | Submission name | Abstract | Contributors |
|---|---|---|---|
| Task Version | symMono | ||
| EN1 | Seq2SeqP4P | Eric Nichols | |
| FC1 | BachProp | Florian Colombo | |
| MM1 | First-order Markov model | Task captains | For purposes of comparison |
| Task Version | symPoly | ||
| FC1 | BachProp | Florian Colombo | |
| MM1 | First-order Markov model | Task captains | For purposes of comparison |
Table 1. Algorithms submitted to Patterns for Prediction 2018. Seg2SegPvP and BachProp are models based on LSTM networks.
Results
We measure the performance of an algorithm to 1) predict a continuation, given a prime (explicit task), and 2) decide which of two versions is the true or foil continuation, given a prime (implicit task). To evaluate performance at the explicit task, we compare the true continuation to the generated continuation, and measure how many pitches and inter-onset intervals (with relation to the last onset of the prime) are correctly predicted at various time intervals after the last note of the prime. To evaluate performance at the implicit task, we measure accuracy as the number of correct decisions, divided by the total amount of decisions. (For mathematical definitions of the various metrics, please see 2018:Patterns_for_Prediction#Evaluation_Procedure.)
SymMono
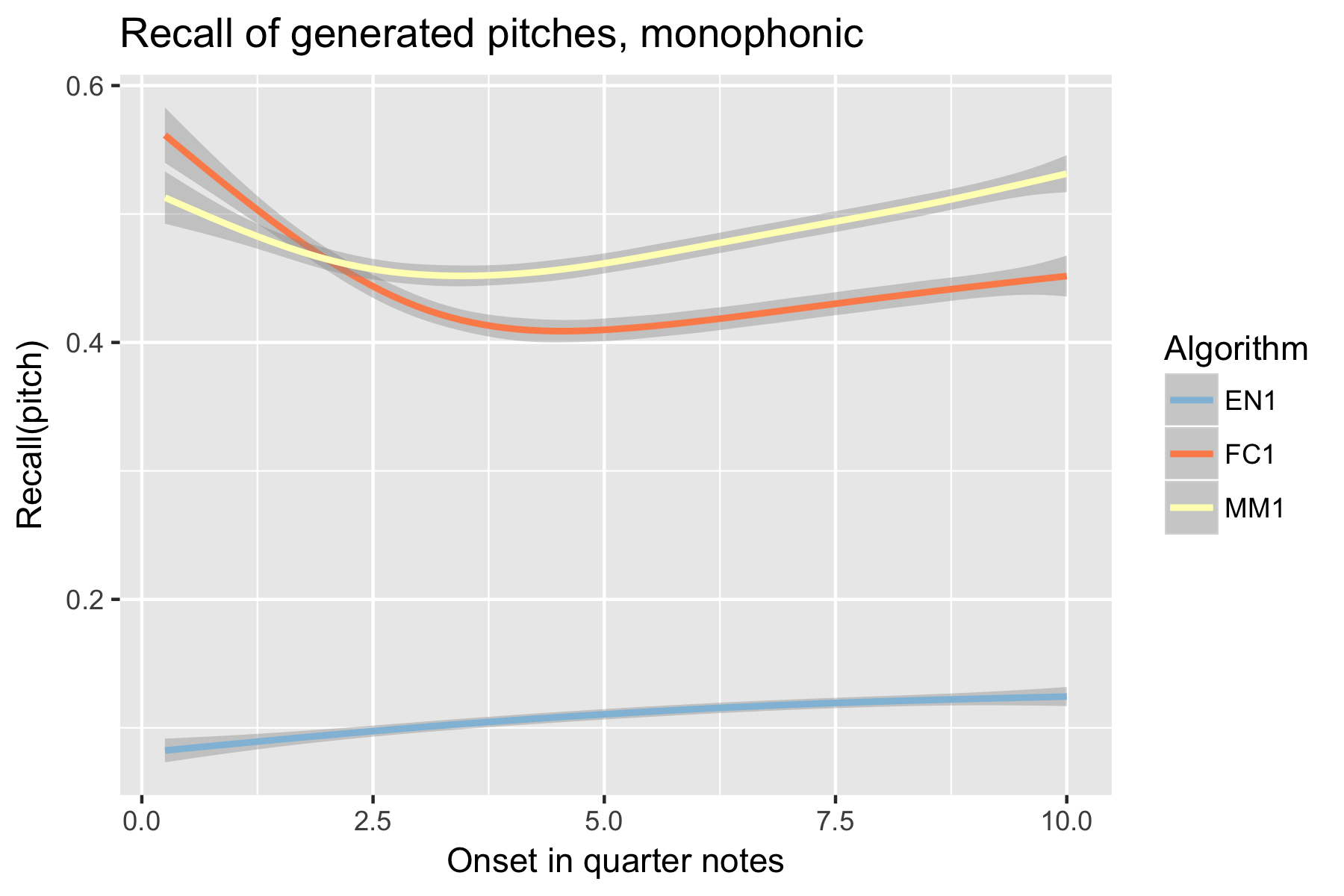
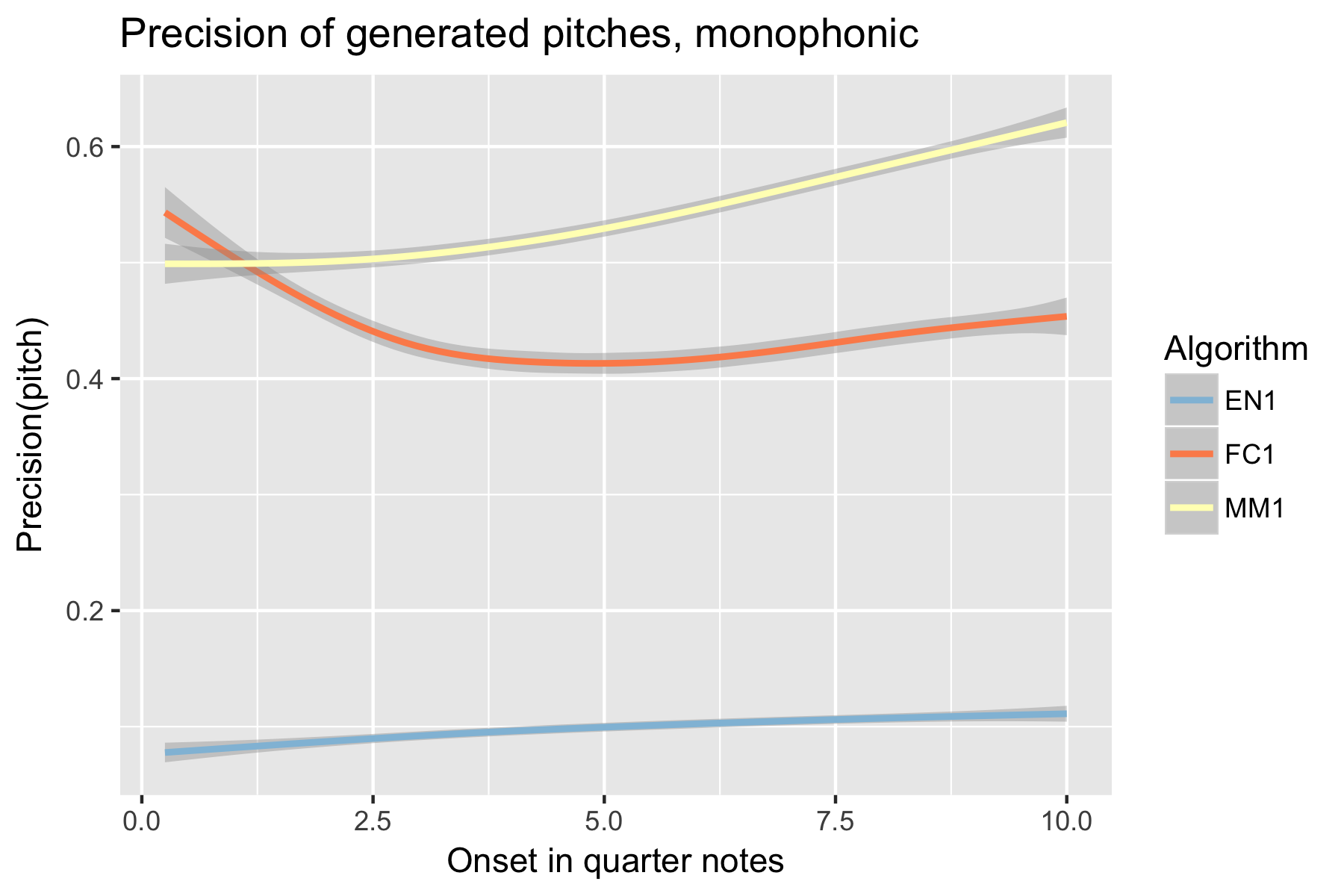
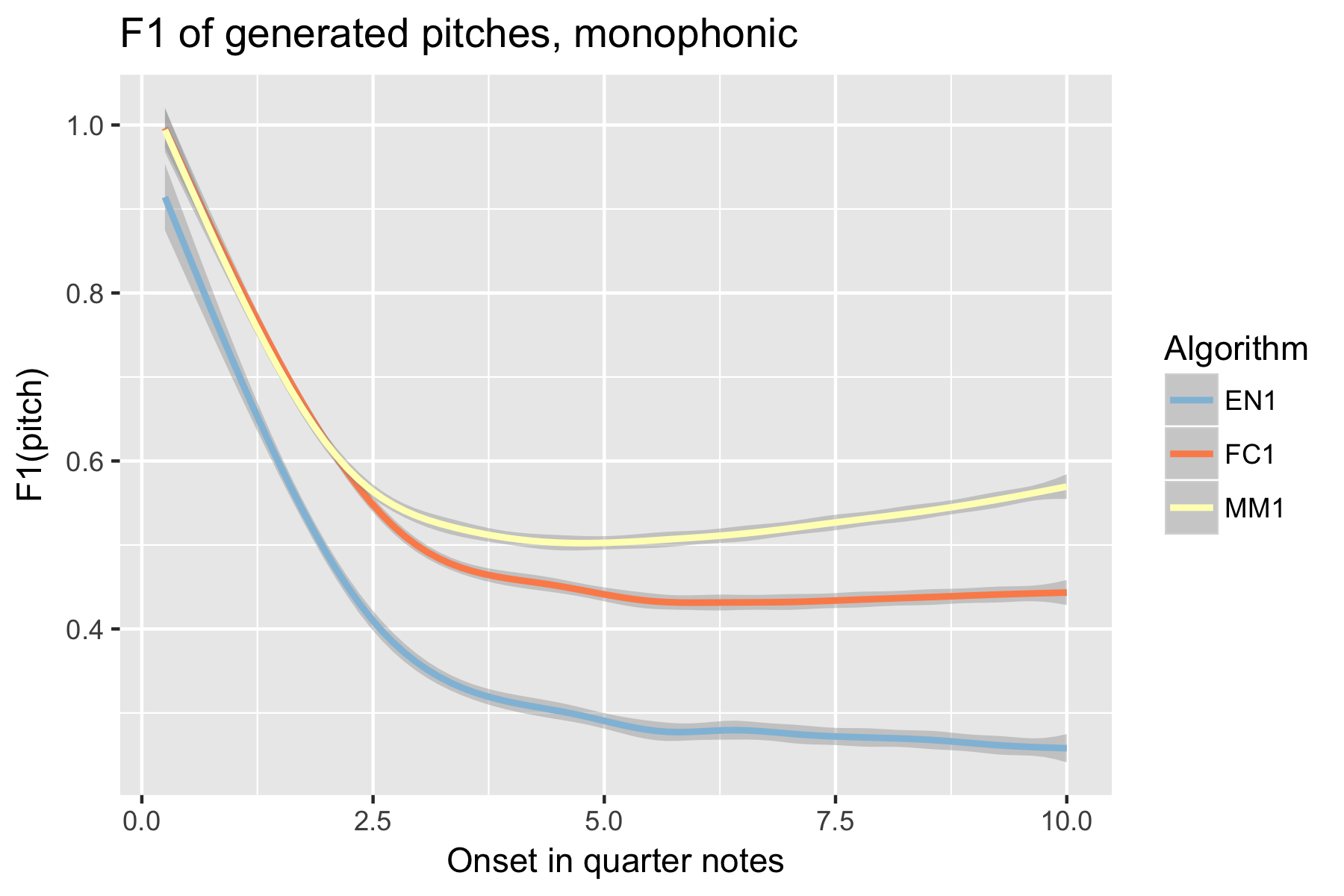
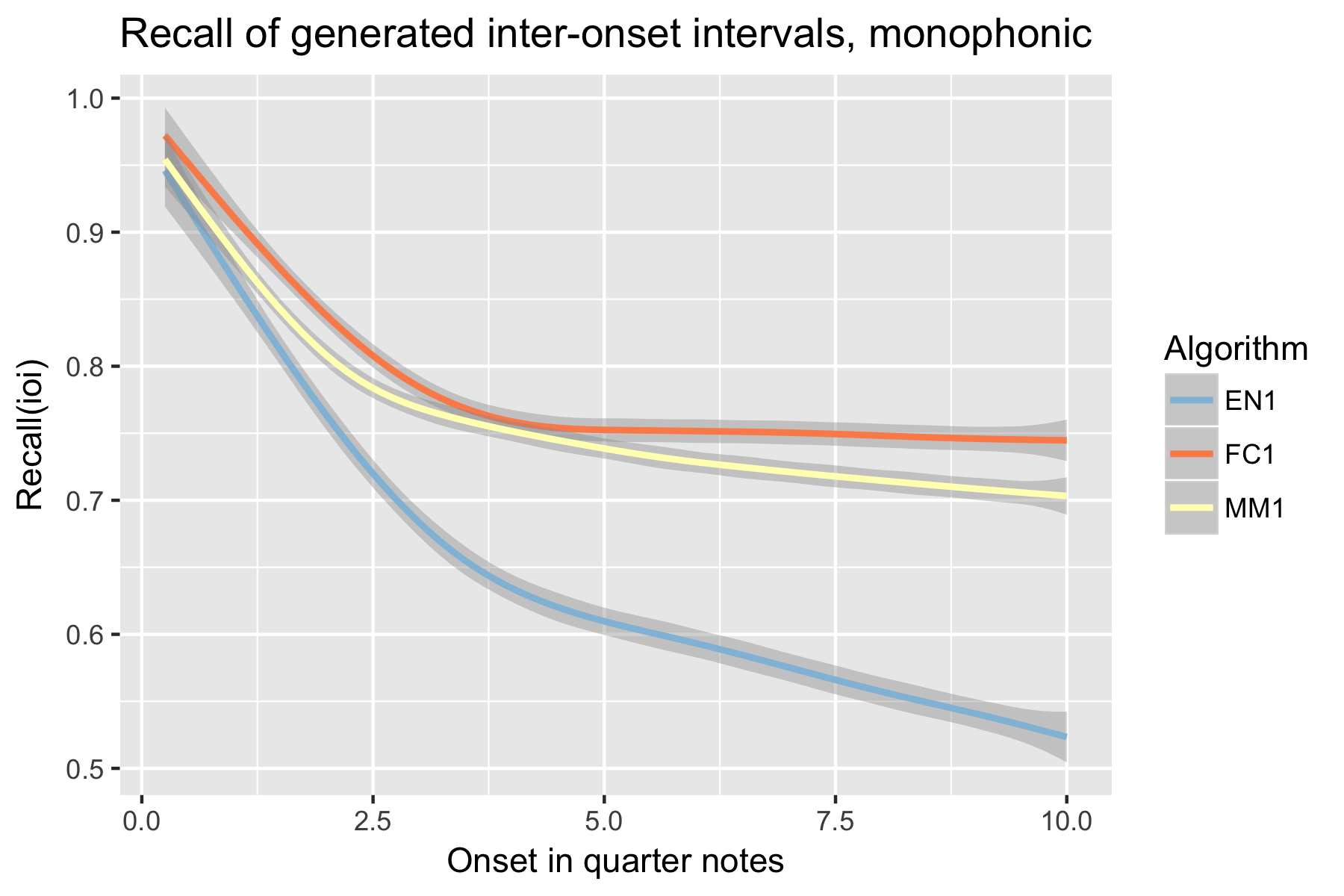
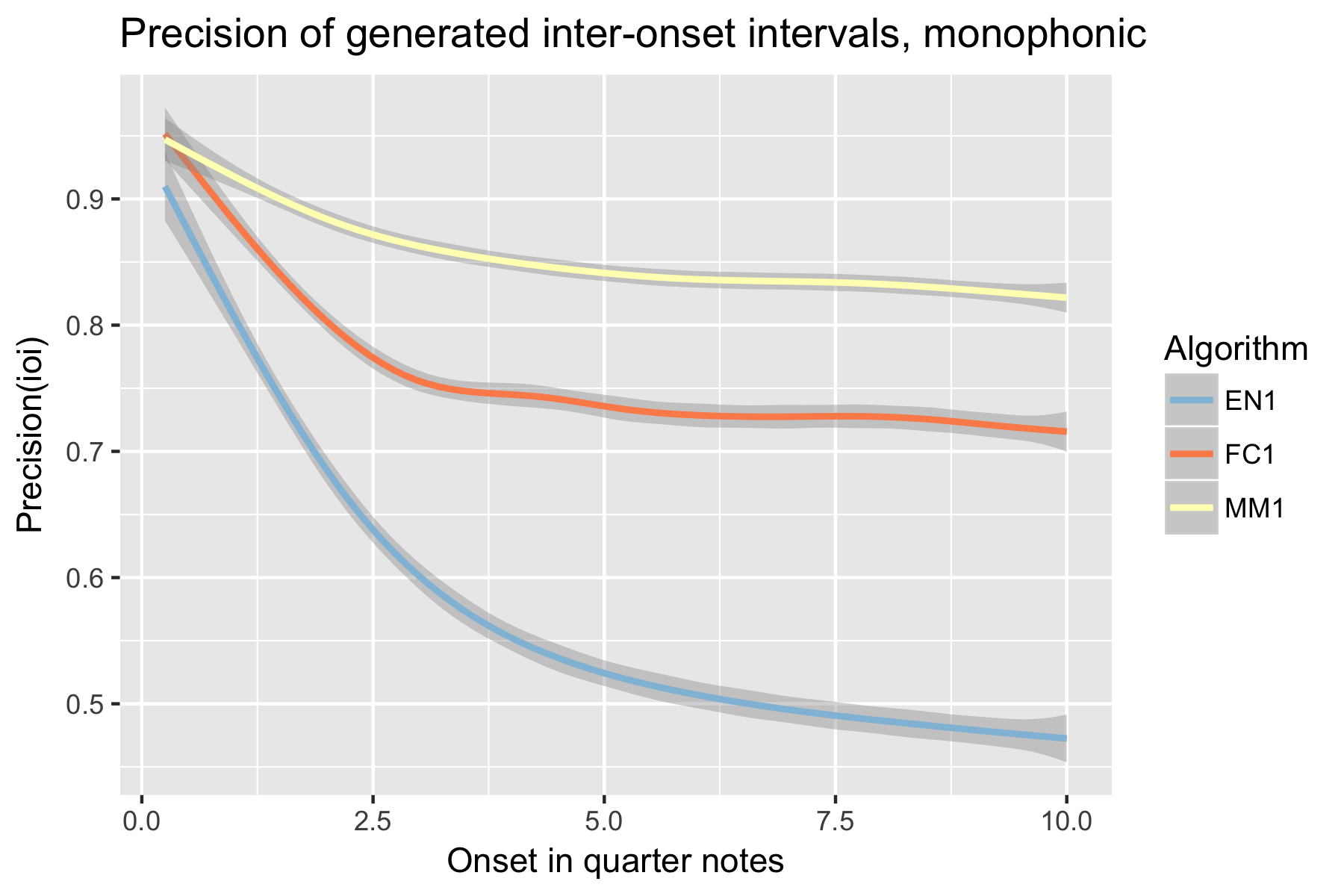
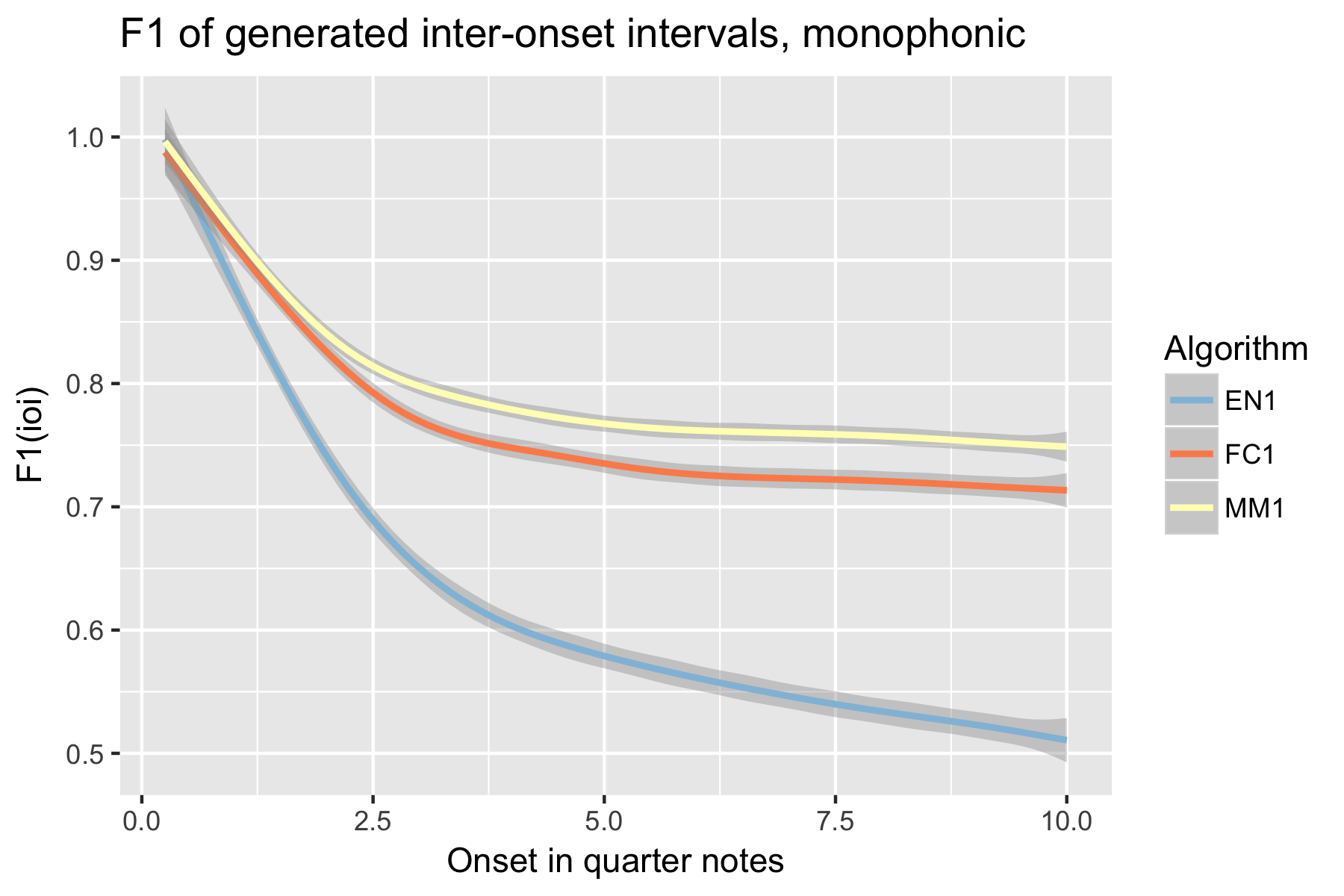
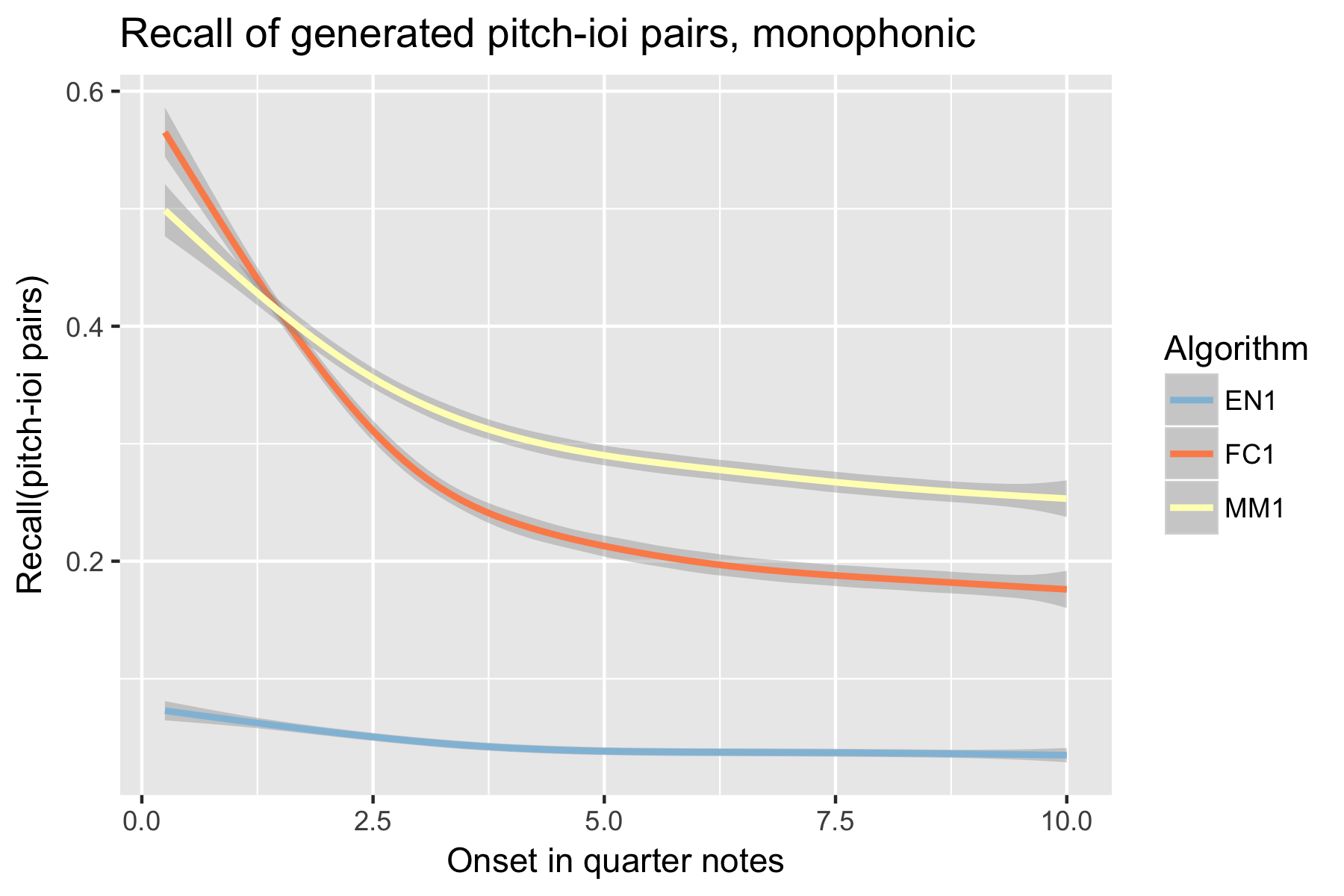
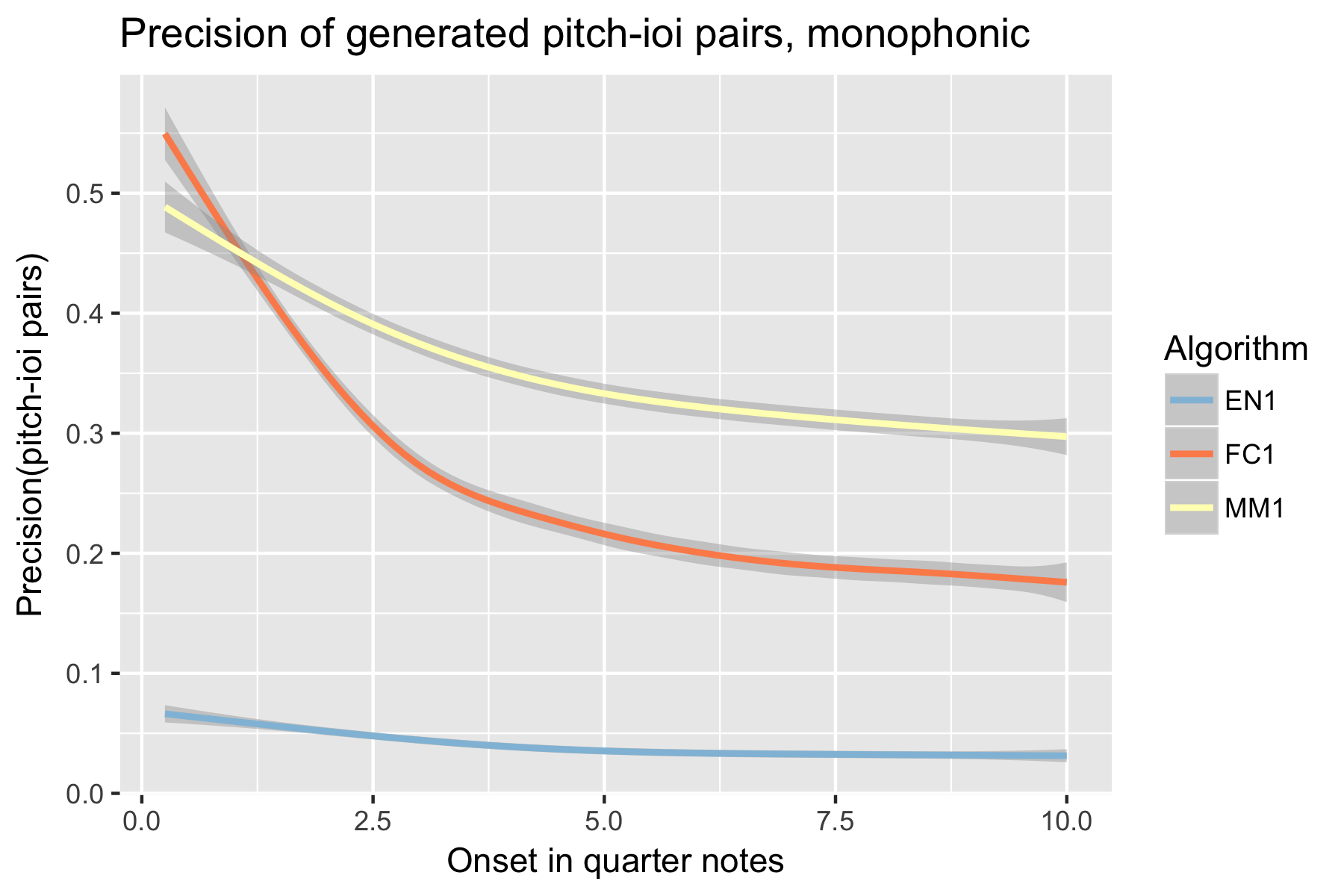
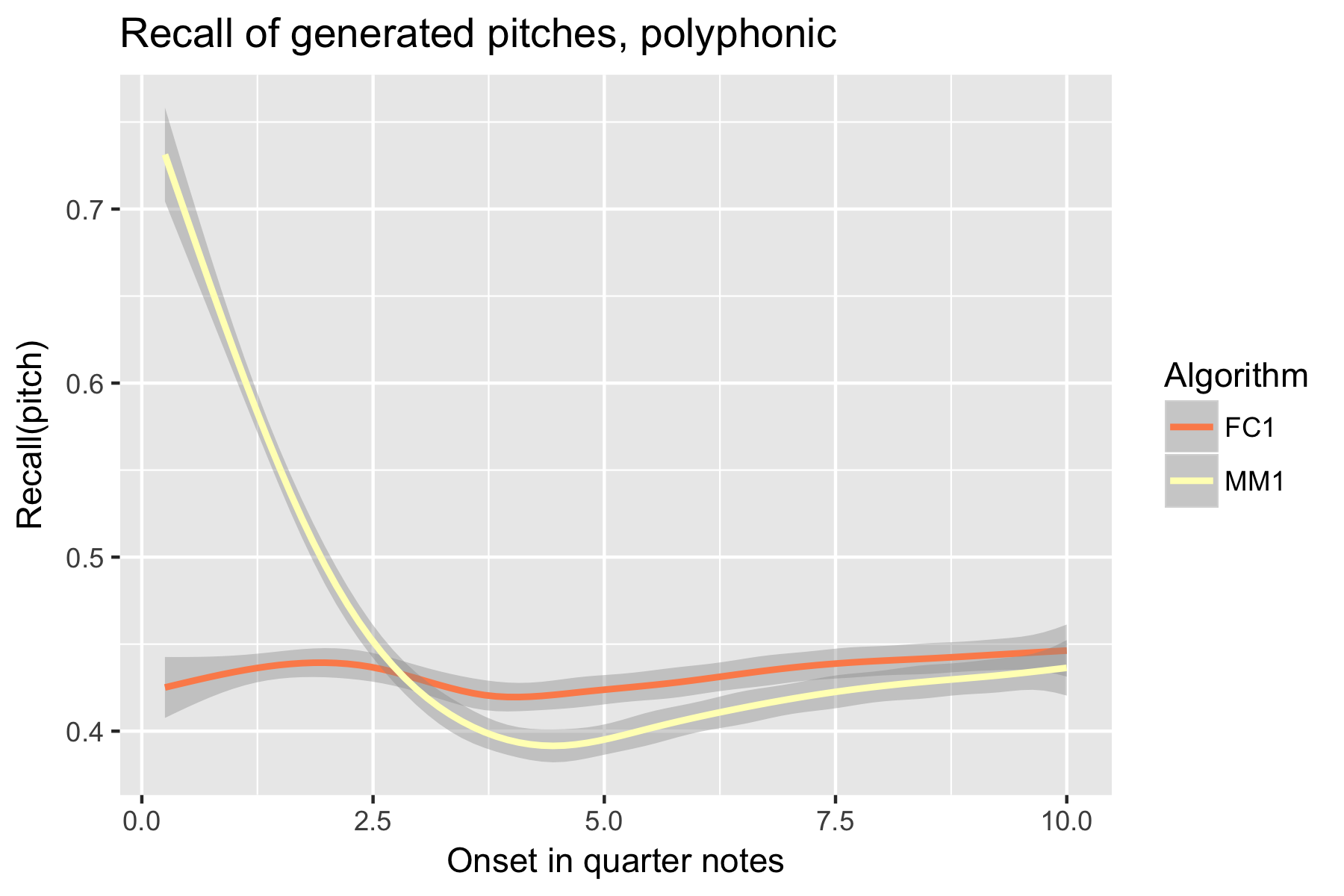
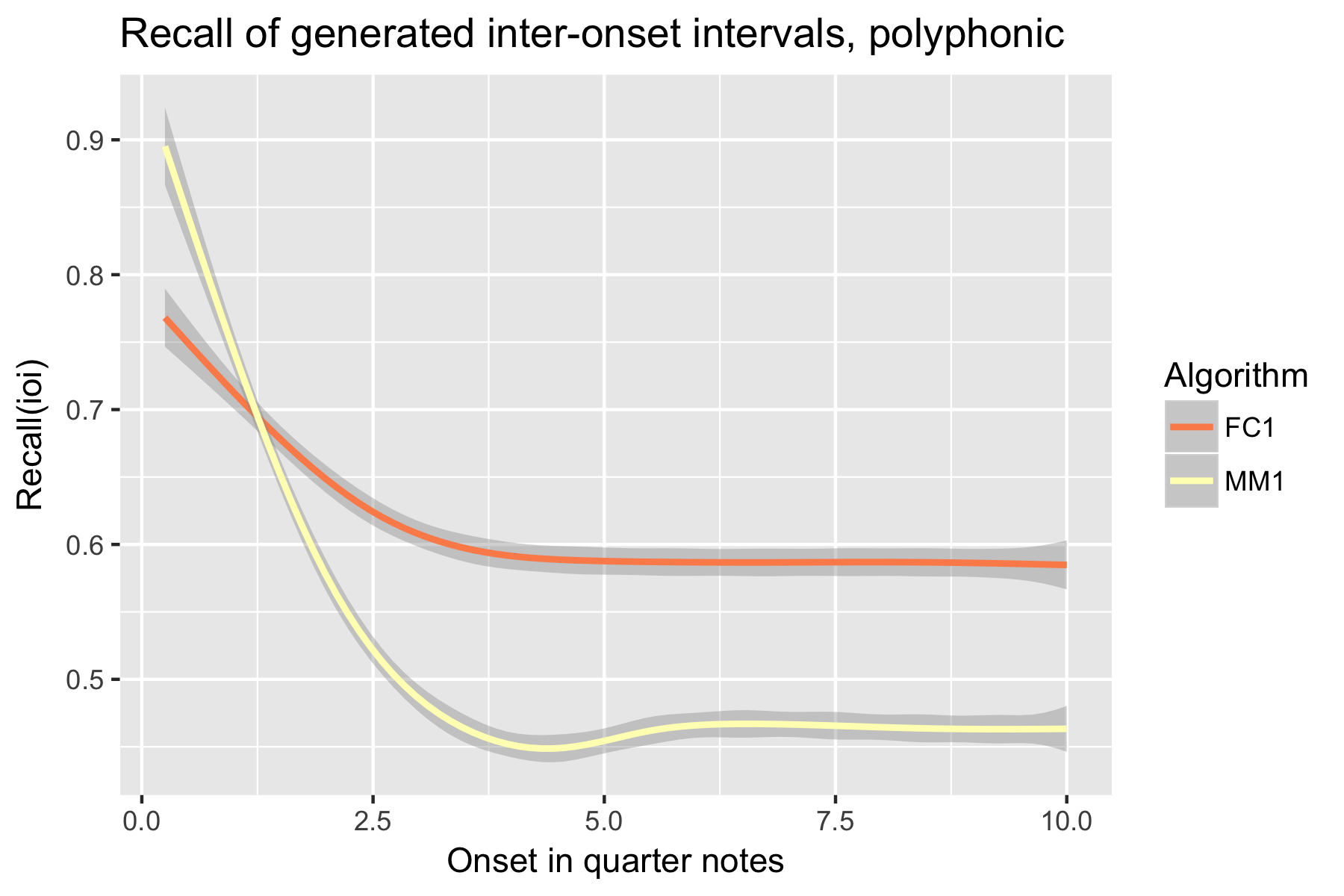
For the implicit task, the two LSTM based models make their best predictions close to the cut-off point (i.e., last event of the prime). As the onset time after the cut-off point increases, the Markov Model outperforms the LSTM based models, with the exception of recall of inter-onset interval (cf. Figure 4), where FC1 consistently performs better than the Markov Model. Possibly in consequence of the poorer pitch performance, also fewer relevant pitch-ioi pairs were detected by the LSTM models as onset time after cutoff point increases.
For the explicit task, only FC1 was submitted. It outperforms chance level significantly, at 0.87, i.e., picking the correct continuation in almost 90% of the cases (See Table 1).
SymPoly
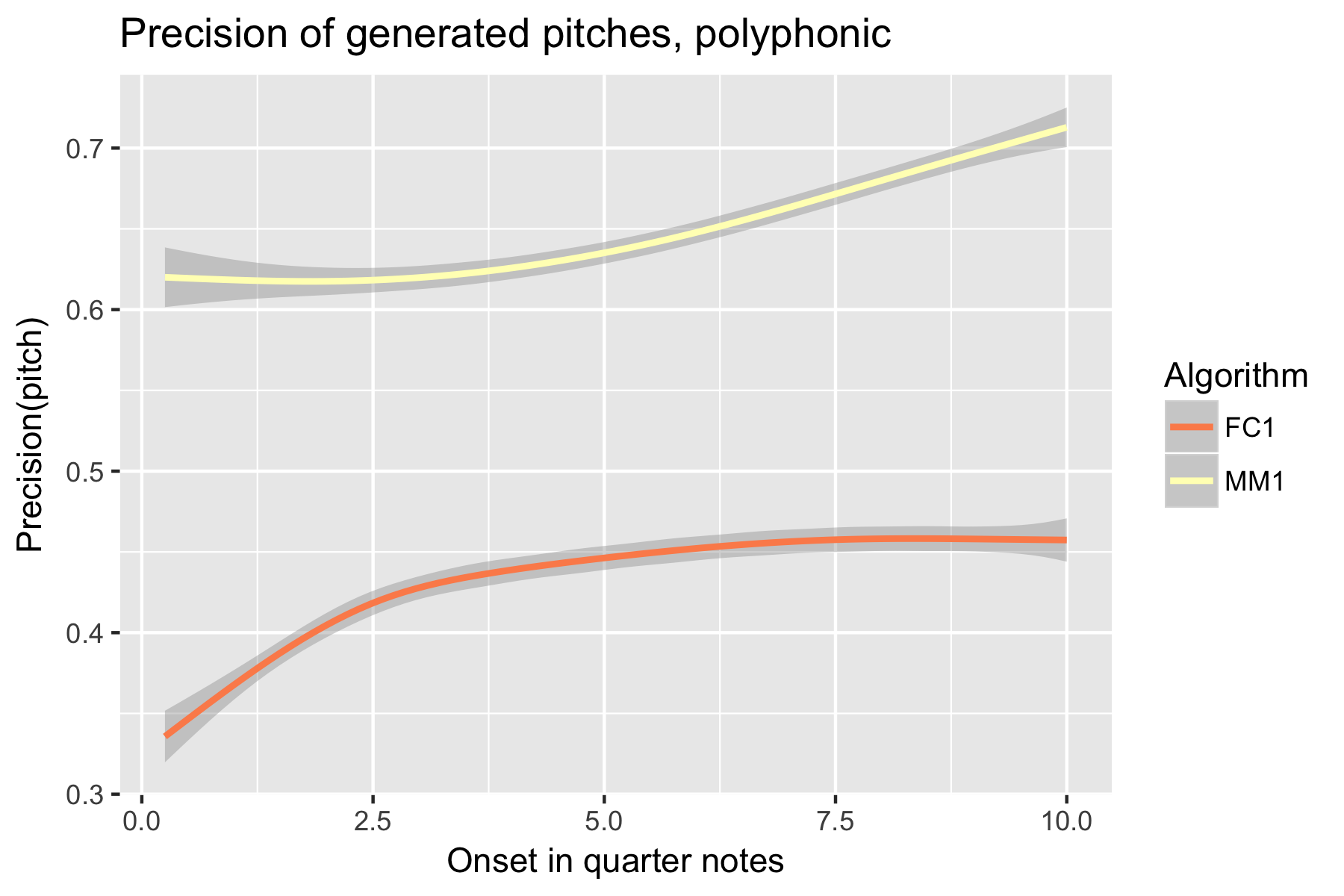
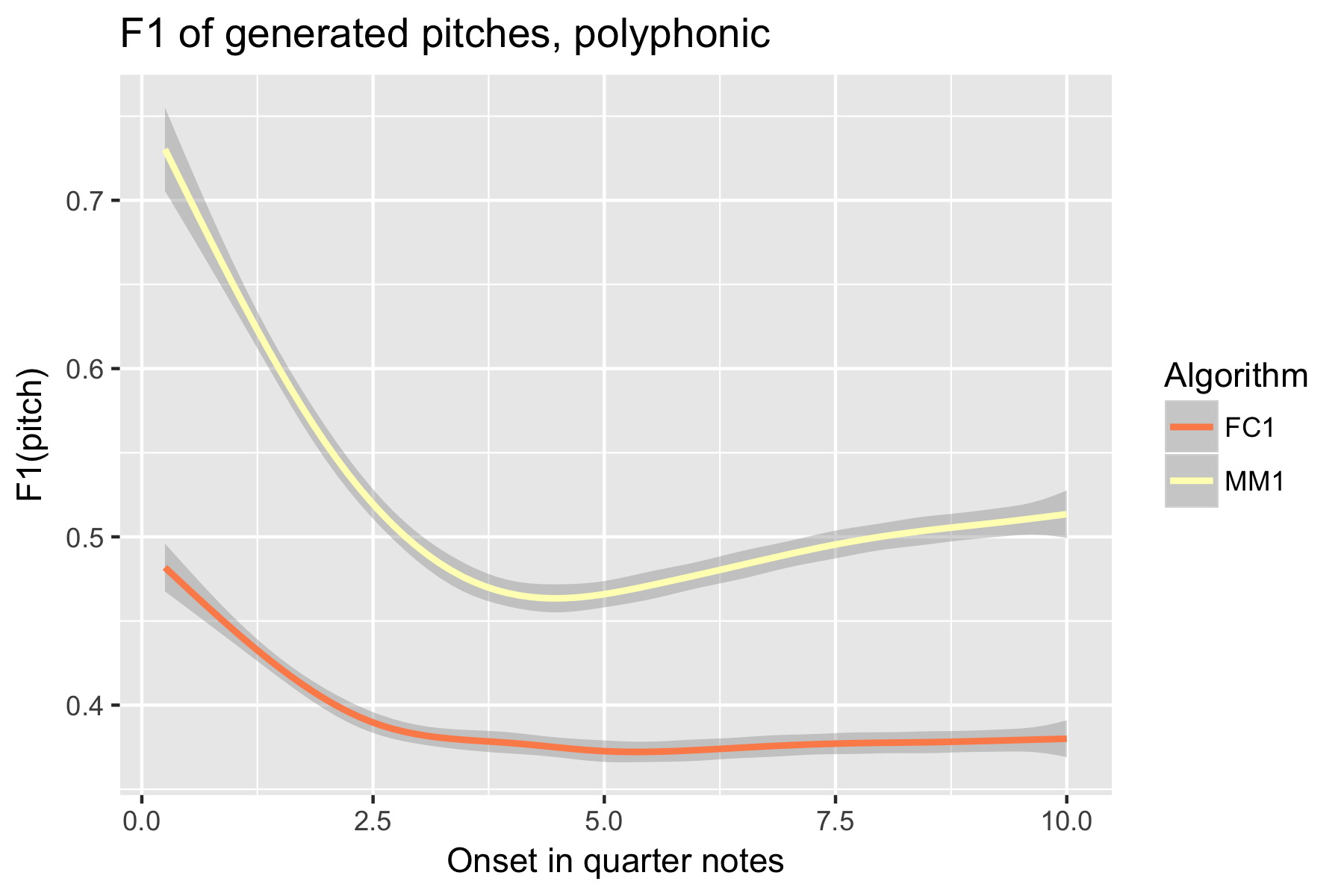
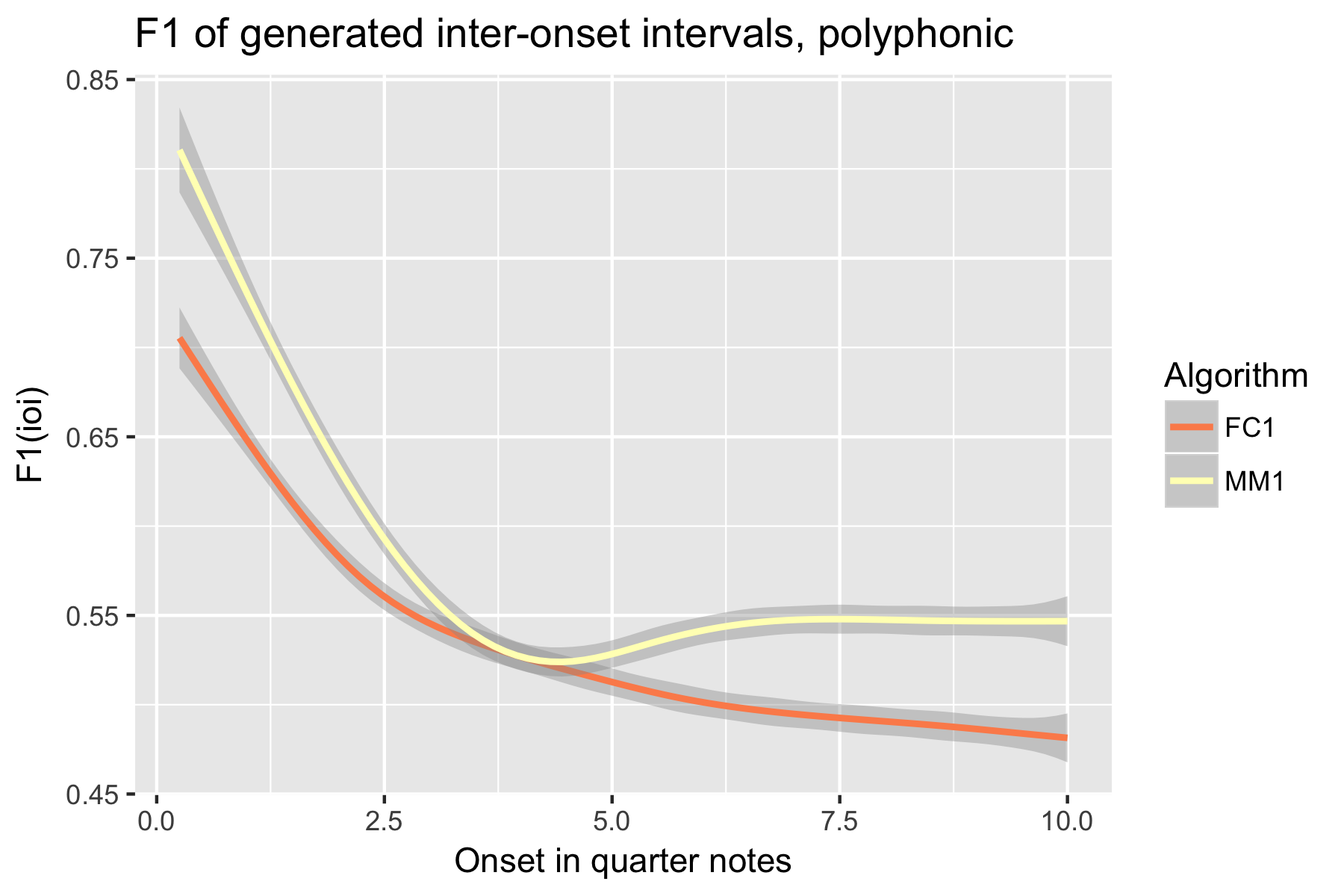
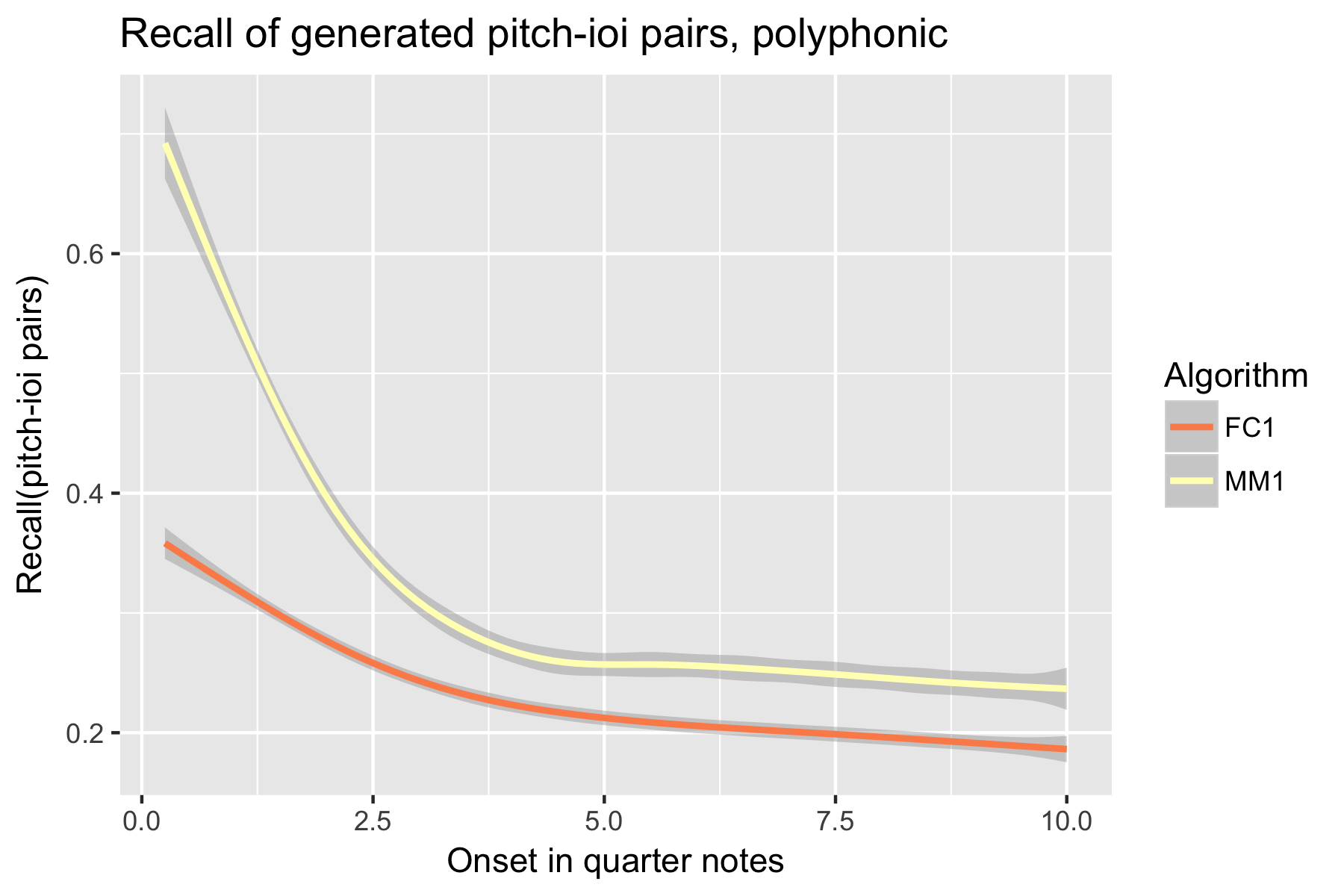
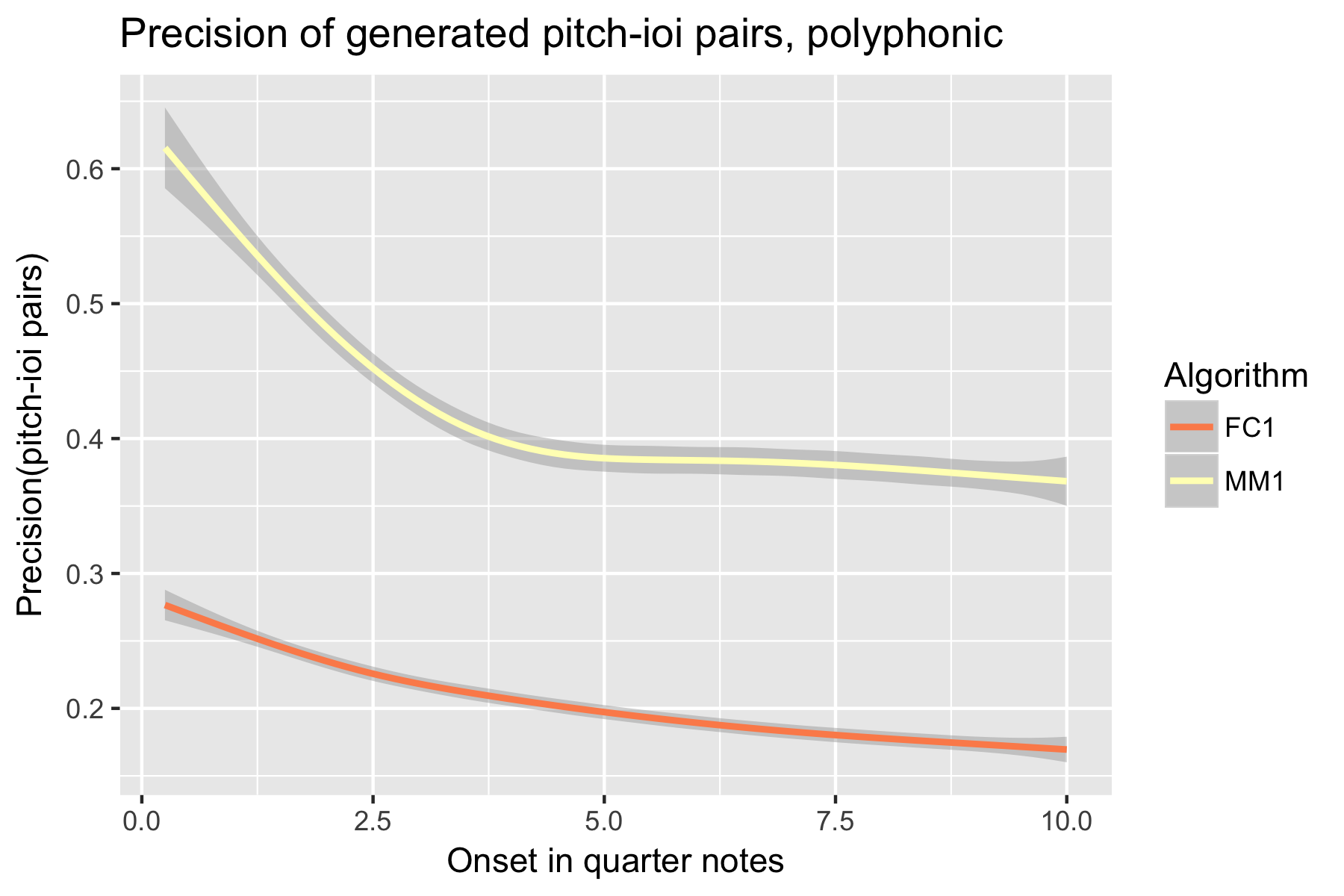
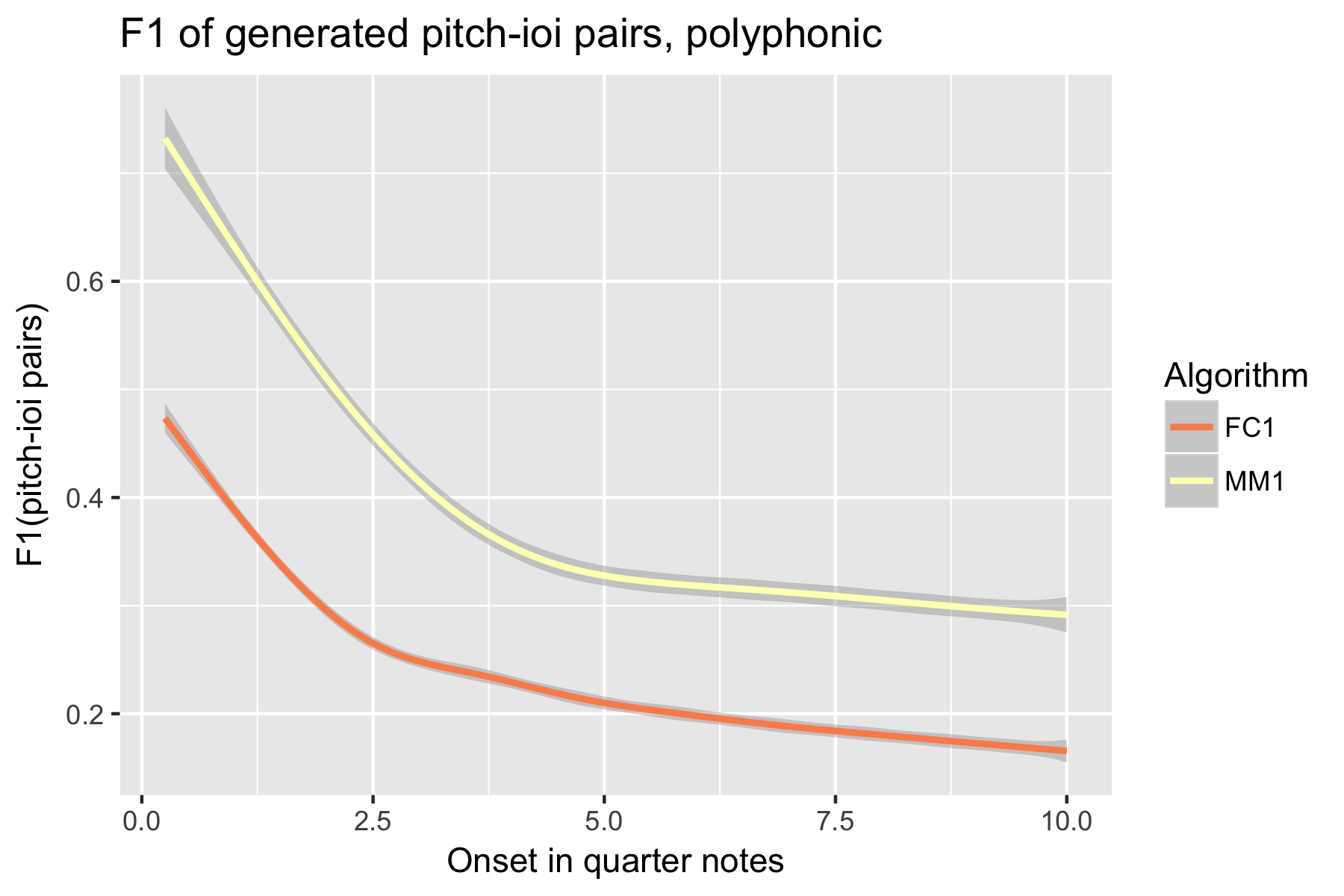
Only one LSTM model was submitted to SymPoly (FC1), with results comparable to SymMono (see Figures 10-18, Table 1).
Figures
symMono
Explicit task: generate music given a prime
Figure 1. Recall of generated pitches after cutoff point.
Figure 2. Precision of generated pitches after cutoff point.
Figure 3. F1 measure of generated pitches after cutoff point.
Figure 4. Recall of generated inter-onset intervals after cutoff point.
Figure 5. Precision of generated inter-onset intervals after cutoff point.
Figure 6. F1 measure of generated inter-onset intervals after cutoff point.
Figure 7. Recall of generated pitch-ioi pairs after cutoff point.
Figure 8. Precision of generated pitch-ioi pairs after cutoff point.
Figure 9. F1 measure of generated pitch-ioi pairs after cutoff point.
Explicit Task: Polyphonic
Figure 10. Recall of generated pitches after cutoff point.
Figure 11. Precision of generated pitches after cutoff point.
Figure 12. F1 measure of generated pitches after cutoff point.
Figure 13. Recall of generated inter-onset intervals after cutoff point.
Figure 14. Precision of generated inter-onset intervals after cutoff point.
Figure 15. F1 measure of generated inter-onset intervals after cutoff point.
Figure 16. Recall of generated pitch-ioi pairs after cutoff point.
Figure 17. Precision of generated pitch-ioi pairs after cutoff point.
Figure 18. F1 measure of generated pitch-ioi pairs after cutoff point.
Tables
Implicit task: decide which of two continuations is the true one, given the prime
| Algorithm | Monophonic | Polyphonic |
|---|---|---|
| FC1 | 0.87 | 0.92 |
| Sig. > chance | 0.54 | 0.54 |